
【题目】如图,已知在平面直角坐标系xOy中,抛物线![]() 经过原点,且与
经过原点,且与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 的横坐标为6,抛物线顶点为点
的横坐标为6,抛物线顶点为点![]() .
.
(1)求这条抛物线的表达式和顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() ,在直线
,在直线![]() 上点取一点
上点取一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将该抛物线向左平移![]() 个单位,所得新抛物线与
个单位,所得新抛物线与![]() 轴负半轴相交于点
轴负半轴相交于点![]() 且顶点仍然在第四象限,此时点
且顶点仍然在第四象限,此时点![]() 移动到点
移动到点![]() 的位置,
的位置,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将点O,点A坐标代入解析式可求抛物线的表达式和顶点B的坐标;
(2)由点A,点B坐标可求直线AB解析式,即可求直线OP解析式为:y=![]() x,设点Q(3k,4k),可证四边形OQAP为等腰梯形,可得OB=QA,由两点距离公式可求k的值,即可求点Q坐标;
x,设点Q(3k,4k),可证四边形OQAP为等腰梯形,可得OB=QA,由两点距离公式可求k的值,即可求点Q坐标;
(3)过点B分别做作x、y轴垂线,垂足分别为点E、F,由题意可证△BCF∽△BDE,可得![]() ,可得
,可得![]() ,可得
,可得![]() ,可得关于m的方程,即可求m的值.
,可得关于m的方程,即可求m的值.
(1)∵点![]() 、
、![]() 在抛物线
在抛物线![]() 上
上
∴ ,解得
,解得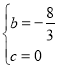
∴抛物线的解析式为![]() ,
,
∴顶点B的坐标是![]() ;
;
(2)如图,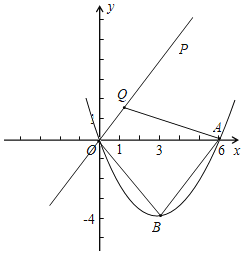
∵![]() ,
,![]()
∴直线AB解析式为:y=![]() x-8,
x-8,
∵![]()
∴直线OP解析式为:y=![]() x,
x,
设点![]() ,
,
∵∠OBA=∠QAB>∠OAB,
∴k>0
∵OP平于AB,QA不平行于OB
∴四边形OQAB为梯形
又∵∠QAB=∠OBA
∴四边形OQAB为等腰梯形
∴QA=OB
∴(6-3k)2+(4k)2=25
∴![]() 或
或![]() (舍去)
(舍去)
∴![]()
(3)由(1)知![]()
设抛物线向左平移![]() 个单位后的新抛物线表达式为
个单位后的新抛物线表达式为![]()
∵新抛物线与y轴负半轴相交于点C且顶点仍然在第四象限,设点C的坐标为C(0,c)
∴0<m<3,-4<c<0,
如图,过点B分别做作x、y轴垂线,垂足分别为点E、F
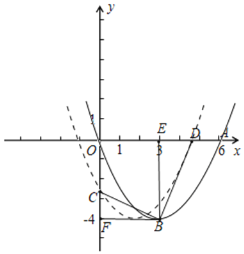
∴![]() 且
且![]()
∴![]() ∽
∽![]()
∴![]()
∴![]()
∴![]()
∴ ![]()
又∵![]()
∴ ![]()
∴ ![]()
∴![]() 或者
或者![]() (舍去)
(舍去)
∴ ![]()


科目:初中数学 来源: 题型:
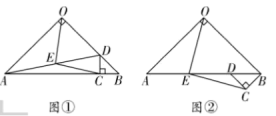
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
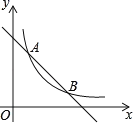
【题目】已知反比例函数y=![]() 与一次函数y=ax+b的图象相交于点A(2,6),和点B(4,m).
与一次函数y=ax+b的图象相交于点A(2,6),和点B(4,m).
(1)求反比例函数与一次函数的解析式;
(2)直接写出不等式![]() ≤ax+b的解集和△AOB的面积.
≤ax+b的解集和△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的顶点
的顶点![]() 在边
在边![]() 上,
上,![]() ,
,![]() 两点分别在边
两点分别在边![]() ,
,![]() 上,且
上,且![]() .将矩形
.将矩形![]() 以每秒1个单位长度的速度沿射线
以每秒1个单位长度的速度沿射线![]() 方向匀速运动,当点
方向匀速运动,当点![]() 与点
与点![]() 重合时停止运动,设运动时间为
重合时停止运动,设运动时间为![]() 秒,矩形
秒,矩形![]() 与
与![]() 重叠部分的面积为
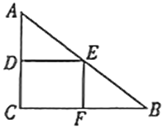
重叠部分的面积为![]() ,则反映
,则反映![]() 与
与![]() 的函数关系的图象为( )
的函数关系的图象为( )
A. B.
B.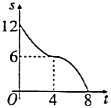 C.
C.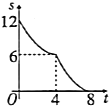 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年初,新冠肺炎肆虐全球.我国政府和人民采取了积极有效的防疫措施,疫情在我国得到了有效控制.小明为复学到药店购买![]() 口罩和一次性医用口罩.已知购买
口罩和一次性医用口罩.已知购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用口罩共需
个一次性医用口罩共需![]() 元;购买
元;购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用罩共需
个一次性医用罩共需![]() 元.
元.
(1)求![]() 口罩与一次性医用口罩的单价;
口罩与一次性医用口罩的单价;
(2)小明准备购买![]() 口罩和一次性医用口罩共
口罩和一次性医用口罩共![]() 个,且
个,且![]() 口罩的数量不少于一次性医用口罩数量的
口罩的数量不少于一次性医用口罩数量的![]() .请设计出最省钱的购买方案,并说明理由.
.请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A是线段BC上一点,△ABD,△AEC都是等边三角形,BE交AD于点M,CD交AE于N.
(1)求证:BE=DC;
(2)求证:△AMN是等边三角形;
(3)将△ACE绕点A按顺时针方向旋转90°,其它条件不变,在图2中补出符合要求的图形,并判断(1)、(2)两小题结论是否仍然成立,并加以证明.
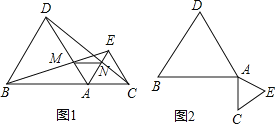
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com