
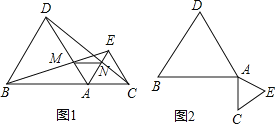
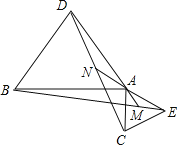
【题目】如图1,点A是线段BC上一点,△ABD,△AEC都是等边三角形,BE交AD于点M,CD交AE于N.
(1)求证:BE=DC;
(2)求证:△AMN是等边三角形;
(3)将△ACE绕点A按顺时针方向旋转90°,其它条件不变,在图2中补出符合要求的图形,并判断(1)、(2)两小题结论是否仍然成立,并加以证明.
【答案】(1)证明见详解;(2)证明见详解;(3)(1)的结论成立,(2)的结论不成立,证明见详解
【解析】
(1)根据等边三角形的性质得到AB=AD,AC=AE,∠DAB=∠EAC=60°,则∠DAC=∠BAE,根据“SAS"可判断△ABE≌△ADC,则BE= DC;
(2)由△ABE≌△ADC得到∠ABE=∠ADC,根据"AAS"可判断△ABM≌△ADN(AAS),则AM=AN;∠DAE=60°,根据等边三角形的判定方法可得到△AMN是等边三角形.
(3)判定结论1是否正确,也是通过证明△ABE≌△ADC求得,这两个三角形中AB=AD,AE=AC,∠BAE和∠CAD都是60°+∠ACB,因此两三角形就全等BE=CD,结论1正确;将△ACE绕点A按顺时针方向旋转90°,则∠DAC> 90°,因此三角形AMN绝对不可能是等边三角形.
解:(1)∵△ABD,△AEC都是等边三角形,
∴AB=AD,AC=AE,∠DAB=∠EAC=60°,
∴∠DAC=∠BAE,
在△ABE和△ADC中,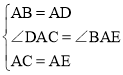 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC;
(2)由上述(1)证得:△ABE≌△ADC,
∴∠ABM=∠ADN.
在△ABM和△ADN中,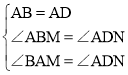 ,
,
∴△ABM≌△ADN(AAS),
∴AM=AN.
∵∠DAE=60°,
∴△AMN是等边三角形;
(3)∵△ABD,△AEC都是等边三角形,
∴AB=AD,AC=AE,∠DAB=∠EAC=60°,
∴∠DAC=∠BAE,
在△ABE和△ADC中,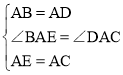 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC,∠ABE=∠ADC,
∵∠BAC=90°
∴∠MAN>90°,
∵∠MAN≠60°,
∴△AMN不是等边三角形,
∴(1)的结论成立,(2)的结论不成立.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线![]() 经过原点,且与
经过原点,且与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 的横坐标为6,抛物线顶点为点
的横坐标为6,抛物线顶点为点![]() .
.
(1)求这条抛物线的表达式和顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() ,在直线
,在直线![]() 上点取一点
上点取一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将该抛物线向左平移![]() 个单位,所得新抛物线与
个单位,所得新抛物线与![]() 轴负半轴相交于点
轴负半轴相交于点![]() 且顶点仍然在第四象限,此时点
且顶点仍然在第四象限,此时点![]() 移动到点
移动到点![]() 的位置,
的位置,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.王先生家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +15 |
(1)王先生这七天中平均每天驾车行驶多少千米?
(2)若每行驶1km需用汽油0.1升,汽油价格为6.5元/升,则王先生家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随杋抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | |
中国诗词大会 |
| 40% |
出彩中国人 | 10 | 20% |
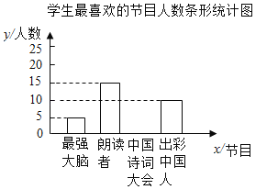
根据以上信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)补全上面的条形统计图;
(3)若该校共有学生![]() 名,估计该校学生最喜爱《朗读者》节目的人数.
名,估计该校学生最喜爱《朗读者》节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉某超市在疫情前用3000元购进某种干果销售,发生疫情后,为了保障附近居民的生活需求,又调拨9000元购进该种干果.受疫情影响,交通等成本上涨,第二次的进价比第一次进价提高了20%,但是第二次购进干果的数量是第一次的2倍还多300千克,如果超市先按每千克9元的价格出售,当大部分干果售出后,最后的600千克按原售价的7折售完.售卖结束后,超市决定将盈利的资金捐助给武汉市用于抗击新冠肺炎疫情.那么该超市可以捐助___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新交通法规实施以来,为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
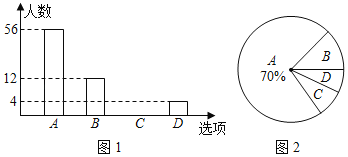
(1)本次调查共选取 名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角是 度,并将条形统计图补充完整;
(3)如果该社区共有居民2600人,估计有多少人从不闯红灯?(请计算说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1.有下列结论:①b2=4ac ②abc>0 ③a>c ④4a+c>2b.其中结论正确的个数是( )
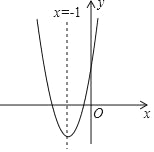
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全国预防“新冠肺炎”时期,某厂接受了生产一批高质量医用口罩的任务.要求8天之内(含8天)生产![]() 型和
型和![]() 型两种型号的口罩共5万只,其中
型两种型号的口罩共5万只,其中![]() 型口罩不得少于1.8万只.该厂的生产能力是:每天只能生产一种型号的口罩,若生产
型口罩不得少于1.8万只.该厂的生产能力是:每天只能生产一种型号的口罩,若生产![]() 型口罩每天能生产0.6万只,若生产
型口罩每天能生产0.6万只,若生产![]() 型口罩每天能生产0.8万只.已知生产6只
型口罩每天能生产0.8万只.已知生产6只![]() 型和10只
型和10只![]() 型口罩一共获利6元,生产4只
型口罩一共获利6元,生产4只![]() 型和5只
型和5只![]() 型口罩一共获利3.5元
型口罩一共获利3.5元
(1)生产一只![]() 型口罩和
型口罩和![]() 型口罩分别获利多少钱?
型口罩分别获利多少钱?
(2)若生产![]() 型口罩
型口罩![]() 万只,该厂这次生产口罩的总利润为
万只,该厂这次生产口罩的总利润为![]() 万元,请求出
万元,请求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在完成任务的前提下,如何安排生产![]() 型和
型和![]() 型口罩的只数,使获得的总利润最大?最大利润是多少?
型口罩的只数,使获得的总利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com