

分析 (1)证明△FAB≌△EAD,根据全等三角形的性质证明结论;
(2)连接AN,作NM⊥BC于M,证明△AKM∽△BKF,根据相似三角形的性质和判定得到△AKF∽△NKB,求出∠NBM=45°,根据等腰直角三角形的性质和三角形中位线定理解答即可;
(3)过点D作DR⊥QD交BC的延长线于R,证明△QAD≌△RCD,得到△DQR是等腰直角三角形,得到答案.
解答 (1)证明:∵AF⊥AE,∠BAD=90°,
∴∠FAB=∠EAD,
在△FAB和△EAD中,
$\left\{\begin{array}{l}{∠FAB=∠EAD}\\{AB=AD}\\{∠ABF=∠ADE}\end{array}\right.$,
∴△FAB≌△EAD,
∴AE=AF;
(2)解:如图1,连接AN,作NM⊥BC于M,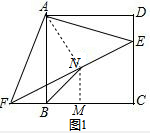 则NM∥CD,又点N是FE的中点,
则NM∥CD,又点N是FE的中点,
∴CE=2MN,
∵∠AKN=∠FKB,∠ANF=∠MNB=90°,
∴△AKM∽△BKF,
∴$\frac{FK}{AK}$=$\frac{BK}{NK}$,又∠AKF=∠NKB,
∴△AKF∽△NKB,
∴∠NBK=∠AFK=45°,
∴∠NBM=45°,
∴BN=$\sqrt{2}$MN,
∴$\frac{BN}{CE}$=$\frac{\sqrt{2}}{2}$;
(3)解:如图2,过点D作DR⊥QD交BC的延长线于R,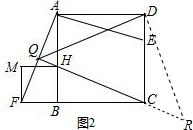 ∵四边形BFMH是正方形,
∵四边形BFMH是正方形,
∴BH=BF,
在△ABF与△CBH中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠CBH}\\{BF=BH}\end{array}\right.$,
∴△ABF≌△CBH,
∴∠BAF=∠BCH,又∠AHQ=∠CHB,
∴∠AQH=∠ABC=90°,
∵∠AHC=∠AQH+∠BAF,∠QAD=∠BAF+∠BAD,
∴∠AHC=∠QAD,
∵AB∥CD,
∴∠AHC=∠DCR,
∴∠DCR=∠QAD,
∵∠ADC=∠QDR=90°,
∴∠ADQ=∠CDR,
在△QAD和△DCR中,
$\left\{\begin{array}{l}{∠QAD=∠DCR}\\{AD=CD}\\{∠ADQ=∠CDR}\end{array}\right.$,
∴△QAD和△RCD,
∴DQ=DR,
∴∠CQD=45°.
点评 本题主要考查了正方形的性质、等腰直角三角形的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质等知识点,正确的做出辅助线是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
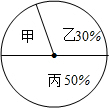 某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )
某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )| A. | 甲对应扇形的圆心角为72° | B. | 学生的总人数是900人 | ||
| C. | 甲比丙地区人数少180人 | D. | 丙比乙地区人数多180人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
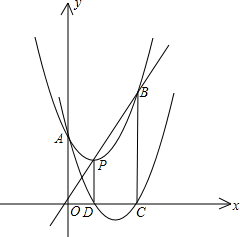 若将抛物线F:抛物线y=x2+bx$\frac{9}{2}$改成y=ax2+bx+c,抛物线的顶点为P,与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C.且a、b、c满足了b2=2ac
若将抛物线F:抛物线y=x2+bx$\frac{9}{2}$改成y=ax2+bx+c,抛物线的顶点为P,与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C.且a、b、c满足了b2=2ac查看答案和解析>>
科目:初中数学 来源: 题型:填空题
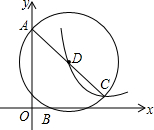 如图,平面直角坐标系中,已知A(0,3),B(1,0),点C在第一象限,⊙D经过点A、B、C三点,AC是⊙O的直径,双曲线y=$\frac{k}{x}$(x>0)经过D、C两点,则k的值是4.
如图,平面直角坐标系中,已知A(0,3),B(1,0),点C在第一象限,⊙D经过点A、B、C三点,AC是⊙O的直径,双曲线y=$\frac{k}{x}$(x>0)经过D、C两点,则k的值是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
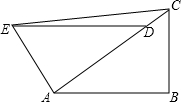 如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE
如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com