
����Ŀ��ij������Ӽס���������Ա����ͬ�������¸����10�Σ�ÿ����ҵijɼ������ͼ��ʾ��
��1���뽫�±��������������ο���ʽ������S2=![]() [��x1��
[��x1��![]() ��2+��x2��
��2+��x2��![]() ��2+��+��xn��
��2+��+��xn��![]() ��2]��
��2]��
ƽ���� | ���� | ��λ�� | |
�� | 7 | �� �� | 7 |
�� | �� �� | 5.4 | �� �� |
��2���������������ͬ�ĽǶȶ���β��Խ������
�ٴ�ƽ�����ͷ������Ͽ����� ���ijɼ���Щ��
�ڴ�ƽ��������λ�����Ͽ����� ���ijɼ���Щ��
����������ѡ����óɼ���9�����ң���Ҫѡһ�˲���������Ϊѡ˭�μӣ���˵�����ɣ�

���𰸡���1��1.2��7��7.5����2���ף��ң��ң����ɼ�����.
������������: ��1������ͳ�Ʊ������ƽ�����������λ���Ķ��壬���������Ҫ��д�����ݣ�
��2�����ɷֱ��ƽ�����ͷ������������ֽ��бȽϣ�
���ɷֱ��ƽ��������λ�����������ֽ��бȽϣ�
���ɴӾ���������ֵ����˵�����ɣ�
���:
�⣺��1���ķ���![]() [��9��7��2+��5��7��2+4����7��7��2+2����8��7��2+2����6��7��2]=1.2��
[��9��7��2+��5��7��2+4����7��7��2+2����8��7��2+2����6��7��2]=1.2��
�ҵ�ƽ��������2+4+6+8+7+7+8+9+9+10����10=7��
�ҵ���λ������7+8����2=7.5��
������£�
ƽ���� | ���� | ��λ�� | |
�� | 7 | 1.2 | 7 |
�� | 7 | 5.4 | 7.5 |
��2���ٴ�ƽ�����ͷ������Ͽ����ijɼ���Щ��
�ڴ�ƽ��������λ�����Ͽ����ҵijɼ���Щ��
��ѡ�Ҳμ���
���ɣ��ۺϿ������Ӹ��ȶ�����������Ȳ�ҷ�����Ȼ���ȶ��������и߰л��������࣬�ɼ������������DZ��������������ֵ��Ӧѡ�ң�
�ʴ�Ϊ����1��1.2��7��7.5����2���ټף����ң�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з����У�һԪ���η��̵ĸ����ǣ�������
��3x2+7=0����ax2+bx+c=0���ۣ�x��2����x+5��=x2��1����3x2��![]() =0��
=0��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
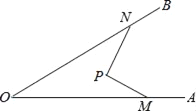
����Ŀ����ͼ����AOB=30�㣬P������AOB�ڲ���M��������OA�ϣ����߶�PM��P����ʱ����ת90�㣬M��ǡ������OB�ϵ�N�㣨OM��ON������PM=![]() ��ON=8����OM=_____��
��ON=8����OM=_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������1����Ҫ��2��2Ů��4��ͬѧ��ѡ��������������֣�
��1��������4�������ѡ1�ˣ�����ѡ��ͬѧ�Ա�Ϊ�����ĸ������� ����
��2��������4�������ѡ2�ˣ�����2��ͬѧ�Ա���ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������У�����֤����ABD�ա�ACD���ǣ� ��.

A.BD=DC�� AB=AC B.��ADB=��ADC��BD=DC
C.��B=��C����BAD=��CAD D. ��B=��C��BD=DC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
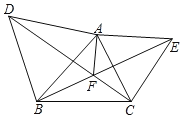
����Ŀ����ͼ���ֱ��ԡ�ABC�ı�AB��AC�����������ȱ������Ρ�ABD����ACE������BE��CD����F������AF��
��1����֤����ACD�ա�AEB��
��2����֤��AF+BF+CF=CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��a��0����ͼ����ͼ��ʾ��
��a��0����ͼ����ͼ��ʾ��
���������
��a��bͬ����
����x=1��x=3ʱ������ֵ�����
��4a+b=0��
����-1��x��5ʱ��y��0��
������ȷ������ ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
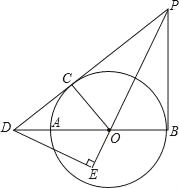
����Ŀ����ͼ��ABΪ��O��ֱ����PD�С�O�ڵ�C����BA���ӳ��߽��ڵ�D��DE��PO��PO�ӳ����ڵ�E������PB����EDB=��EPB��
��1����֤��PB�ǡ�O�����ߣ�
��2����PB=3��DB=4����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��BAC��ƽ���߽�BC�ڵ�D����O��AB�ϣ��Ե�OΪԲ�ģ�OAΪ�뾶��Բǡ�þ�����D���ֱ�AC��AB�ڵ�E��F��
��1�����ж�ֱ��BC���O��λ�ù�ϵ����˵�����ɣ�
��2����BD=2![]() ��BF=2������Ӱ���ֵ��������������У���
��BF=2������Ӱ���ֵ��������������У���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com