
【题目】每年5月份是心理健康宣传月,某中学开展以“关心他人,关爱自己”为主题的心理健康系列活动.为了解师生的心理健康状况,对全体2000名师生进行了心理测评,随机抽取20名师生的测评分数进行了以下数据的整理与
①数据收集:抽取的20名师生测评分数如下
85,82,94,72,78,89,96,98,84,65,73,54,83,76,70,85,83,63,92,90.
②数据整理:将收集的数据进行分组并评价等第:
分数x |
|
|
|
|
|
人数 | 5 | a | 5 | 2 | 1 |
等第 |
|
|
|
|
|
③数据绘制成不完整的扇形统计图:
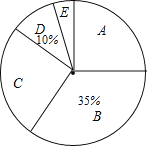
④依据统计信息回答问题
(1)统计表中的 .
(2)心理测评等第![]() 等的师生人数所占扇形的圆心角度数为 .
等的师生人数所占扇形的圆心角度数为 .
(3)学校决定对![]() 等的师生进行团队心理辅导,请你根据数据分析结果,估计有多少师生需要参加团队心理辅导?
等的师生进行团队心理辅导,请你根据数据分析结果,估计有多少师生需要参加团队心理辅导?
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,AB,CD是圆O的直径,AE是圆O的弦,且AE∥CD,过点C的圆O切线与EA的延长线交于点P,连接AC.
(1)求证:AC平分∠BAP;
(2)求证:PC2=PAPE;
(3)若AE-AP=PC=4,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
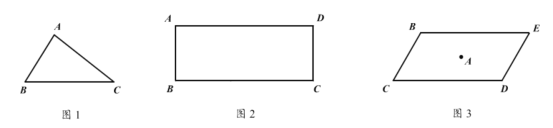
(1)如图1,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;
问题探究:
(2)如图2,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离;
问题解决:
(3)如图3,有一座草根塔A,按规定,要以塔A为对称中心,建一个面积尽可能大的形状为平行四边形的草根景区BCDE。根据实际情况,要求顶点B是定点,点B到塔A的距离为50米,∠CBE=120°,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE?若可以,求出满足要求的平行四边形BCDE的最大面积;若不可以,请说明理由。(塔A的占地面积忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
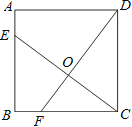
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
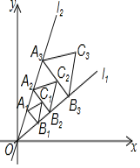
【题目】如图,点A1(1,![]() )在直线l1:y=
)在直线l1:y=![]() x上,过点A1作A1B1⊥l1交直线l2:y=
x上,过点A1作A1B1⊥l1交直线l2:y=![]() x于点B1,A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第2019个等边三角形
x于点B1,A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第2019个等边三角形![]() 的面积为_____.
的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,某中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
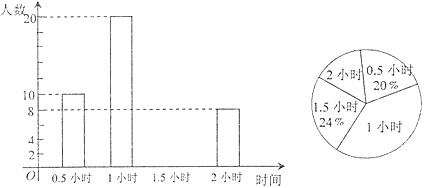
(I).被抽查的学生有_____人,抽查的学生中每天户外活动时间是1.5小时的有_____人;
(II).求被抽查的学生的每天户外活动时间的众数、中位数和平均数;
(III).该校共有1200名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
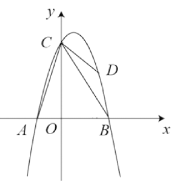
如图,抛物线![]() 经过点A(-2,0),B(4,0)两点,与
经过点A(-2,0),B(4,0)两点,与![]() 轴交于点C,点D是抛物线上一个动点,设点D的横坐标为
轴交于点C,点D是抛物线上一个动点,设点D的横坐标为![]() .连接AC,BC,DB,DC,
.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若点M是![]() 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
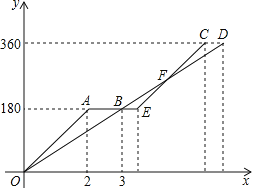
【题目】快车从甲地驶向乙地,慢车从乙地驶向甲地,两车同时出发并且在同一条公路上匀速行驶,途中快车休息1.5小时,慢车没有休息.设慢车行驶的时间为x小时,快车行驶的路程为![]() 千米,慢车行驶的路程为
千米,慢车行驶的路程为![]() 千米.如图中折线OAEC表示
千米.如图中折线OAEC表示![]() 与x之间的函数关系,线段OD表示
与x之间的函数关系,线段OD表示![]() 与x之间的函数关系.
与x之间的函数关系.
请解答下列问题:
(1)求快车和慢车的速度;
(2)求图中线段EC所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)线段OD与线段EC相交于点F,直接写出点F的坐标,并解释点F的实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com