【题目】已知一次函数y1＝kx+m（k≠0）和二次函数y2＝ax2+bx+c（a≠0）的自变最x和对应函数值y1，y2的部分对应值如表：
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y1≥y2时，自变量x的取值范图是_____．
【答案】﹣1≤x≤4
【解析】
根据待定系数法求出两个函数的解析式即可求解．
解：根据表格中的数据可知：
把（﹣1，0）、（0，1）代入一次函数y1＝kx+m中，
得
，解得
，
所以一次函数解析式为y1＝x+1．
∵（﹣1，0）与（3，0）是对称点，
∴抛物线的顶点坐标为（1，﹣4）
所以设抛物线解析式为y＝a（x+1）（x﹣3），
将（1，﹣4）代入，得a＝1，
所以抛物线解析式为y2＝（x+1）（x﹣3）＝x2﹣2x﹣3．
解法一：
当y1＝y2时，即x+1＝x2﹣2x﹣3．
解得x1＝﹣1，x2＝4．
所以两个函数的交点坐标为（﹣1，0）（4，5）；
解法二：
观察表格中的数据可知：．
两个函数的交点坐标为（﹣1，0）（4，5）．
所以当y1≥y2时，自变量x的取值范图是﹣1≤x≤4．
故答案为﹣1≤x≤4．
名校课堂系列答案科目：初中数学 来源： 题型：
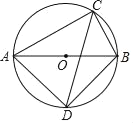
【题目】如图，△ABC内接于⊙O，AB是⊙O直径，∠ACB的平分线交⊙O于D，若AC＝m，BC＝n，则CD的长为_____（用含m、n的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点O在ABCD的AD边上，⊙O经过A、B、C三点，点E在⊙O外，且OE⊥BC，垂足为F．
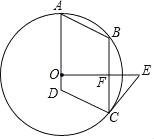
（1）若EC是⊙O的切线，∠A＝65°，求∠ECB的度数；
（2）若OF＝4，OD＝1，求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，△ABC的AB边为圆O的弦，AC、BC分别交圆O于D、E，弧AD=弧BE，∠C=60°；
（1）求证：△ABC为等边三角形；
（2）如图2，F为弧AD上一点，连接FE并延长至G，连接BG，若∠AFB=∠G，求∠FBG的正弦值；
（3）如图3，在（2）的条件下，连接FC并延长交BG延长线于H，若CF=CH，AF=7，HG=12，求线段BF的长度。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝
，y＝﹣2018x2+2019，y＝2018x2共有的性质是（ ）
A.开口向上
B.对称轴是y轴
C.当x＞0时，y随x的增大而增大
D.都有最低点
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝x2+（2m+1）x+m（m﹣3），（m为常数，﹣1≤m≤4），A（﹣m﹣1，y1），
是该抛物线上不同的两点，现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a，过抛物线顶点P作PH⊥a于H．
（1）当m＝1时，求出这条抛物线的顶点坐标；
（2）若无论m取何值，抛物线与直线y＝x﹣km（k为常数）有且仅有一个公共点，求k的值；
（3）当1＜PH≤6时，试比较y1，y2之间的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，AC＝CB，点E，F分别是AC，BC上的点，△CEF的外接圆交AB于点Q，D．
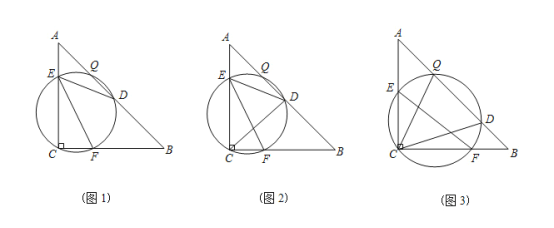
（1）如图1，若点D为AB的中点，求证：∠DEF＝∠B；
（2）在（1）问的条件下：
①如图2，连结CD，交EF于H，AC＝4，若△EHD为等腰三角形，求CF的长度．
②如图2，△AED与△ECF的面积之比是3：4，且ED＝3，求△CED与△ECF的面积之比（直接写出答案）．
（3）如图3，连接CQ，CD，若AE+BF＝EF，求证：∠QCD＝45°．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料:若
，求m、n的值.
解: 
，
，
，
.
根据你的观察，探究下面的问题:
（1）己知
，求
的值.
（2）已知△ABC的三边长a、b、c都是正整数，且满足
，求边c的最大值.
（3） 若己知
，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一圆弧形桥拱的圆心为
，拱桥的水面跨度
米，桥拱到水面的最大高度
为
米．求：
桥拱的半径；
现水面上涨后水面跨度为
米，求水面上涨的高度为________米．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com