
【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180°时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△ABC与△DAE互为“顶补三角形”,AM,AN是“顶心距”.
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,BC=6时,AN的长为 .
猜想论证:
(2)在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,AD=AB,CD=BC,∠B=90°,∠A=60°,CD=2,在四边形ABCD的内部是否存在点P,使得△PAD与△PBC互为“顶补等腰三角形”?若存在,请给予证明,并求△PBC的“顶心距”的长;若不存在,请说明理由.

【答案】(1)①![]() ; ②3;(2)见解析;(3)见解析.
; ②3;(2)见解析;(3)见解析.
【解析】
(1)①只要证明△BAC≌△EAD,推出BC=DE,由AM⊥BC,推出BM=CM,推出AM=![]() BC=
BC=![]() DE;
DE;
②只要证明△AMC≌△DNA,即可解决问题;
(2)结论:DE=2AM,只要证明△AMC≌△DNA即可;
(3)如图4中,结论:存在.连接AC,取AC的中点P,连接PD、PB、作PM⊥BC于M.点P即为所求的点;
(1)①如图2中,
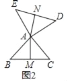
∵AB=AC=AE=AD,∠BAC=∠EAD=90°,
∴△BAC≌△EAD,
∴BC=DE,
∵AM⊥BC,
∴BM=CM,
∴AM=![]() BC=
BC=![]() DE.
DE.
故答案为![]() .
.
②如图3中,
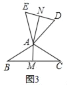
∵∠BAC=120°,AB=AC,AM⊥BC,
∴∠CAM=60°,BM=CM=3
∵∠BAC+∠EAD=180°,
∴∠EAD=60°,
∵AE=AD,
∴△EAD是等边三角形,
∴∠D=60°,
∴∠AMC=∠AND=90°,∠CAM=∠D,AC=AD,
∴△AMC≌△DNA,
∴AN=CM=3,
故答案为3.
(2)如图1中,结论:DE=2AM.
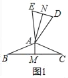
∵AD=AE,AN⊥DE,
∴EN=DN,∠DAN=∠NAE,同法可证:∠CAM=∠BAM,
∵∠BAC+∠EAD=180°,
∴∠DAN+∠CAM=90°,
∵∠CAM+∠C=90°,
∴∠DAN=∠C,
∵∠AND=∠AMC=90°,AC=DA,
∴△AMC≌△DNA,
∴AM=DN,
∴DE=2AM.
(3)如图4中,结论:存在.
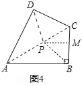
理由:连接AC,取AC的中点P,连接PD、PB、作PM⊥BC于M.
∵AD=AB,CD=CB,AC=AC,
∴△ABC≌△ADC,
∴∠ADC=∠ABC=90°,∠DAC=∠BAC=30°,
∴∠ACD=∠ACB=60°,
∵PA=PC,
∴PA=PD=PC=PB,
∴△PCD,△PCB都是等边三角形,
∴∠CPD=∠CPB=60°,
∴∠APD=120°,
∴∠APD+∠CPB=180°,
∴△APD和△PBC是“顶补等腰三角形”,
在等边三角形△PBC中,∵BC=PC=PB=2,PM⊥BC,
∴PM=![]() ×2=
×2=![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,扇形OMN的圆心角为45°,正方形A1B1C1A2的边长为2,顶点A1,A2在线段OM上,顶点B1在弧MN上,顶点C1在线段ON上,在边A2C1上取点B2,以A2B2为边长继续作正方形A2B2C2A3,使得点C2在线段ON上,点A3在线段OM上,……,依次规律,继续作正方形,则A2018M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌化妆品商店有![]() 、
、![]() 、
、![]() 三种型号的化妆品,今年国庆节期间采用组合打折销售,销售时采用了三种组合的方式进行销售,甲种组合是:
三种型号的化妆品,今年国庆节期间采用组合打折销售,销售时采用了三种组合的方式进行销售,甲种组合是:![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种;乙种组合是:
种;乙种组合是:![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种;丙种组合是:
种;丙种组合是:![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种.如果组合销售打折后A种每盒售价为
种.如果组合销售打折后A种每盒售价为![]() 元,
元,![]() 种每盒售价为
种每盒售价为![]() 元,
元,![]() 种每盒售价为
种每盒售价为![]() 元.国庆节当天,商店采用三种组合搭配的方式进行销售后共得销售额为
元.国庆节当天,商店采用三种组合搭配的方式进行销售后共得销售额为![]() 元,其中
元,其中![]() 种的销售额为
种的销售额为![]() 元,那么
元,那么![]() 种化妆品的销售额是______.
种化妆品的销售额是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
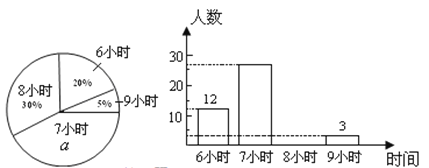
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
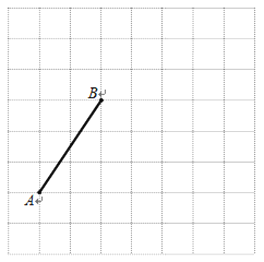
【题目】下图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.
(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,B点的坐标为________________;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为__________________;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c(a≠0)的图象过O、B、C三点,则此函数图象的对称轴方程是________________.
【答案】 (-1,2) (2,0) x=1
【解析】分析:![]() 根据点
根据点![]() 的坐标建立坐标系,即可写出点
的坐标建立坐标系,即可写出点![]() 的坐标.
的坐标.
![]() 画出点
画出点![]() 旋转后的对应点
旋转后的对应点![]() 连接
连接![]() ,写出点
,写出点![]() 的坐标.
的坐标.
![]() 用待定系数法求出函数解析式,即可求出对称轴方程.
用待定系数法求出函数解析式,即可求出对称轴方程.
详解:(1)建立坐标系如图,
B点的坐标为![]() ;
;
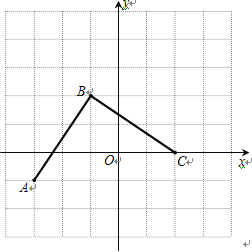
(2)线段BC如图,C点的坐标为![]()
(3)把点![]() 代入二次函数
代入二次函数![]() ,得
,得

解得:
二次函数解析为:![]()
对称轴方程为:![]()
故对称轴方程是![]()
点睛:考查图形与坐标;旋转、对称变换;待定系数法求二次函数解析式,二次函数的图象与性质.熟练掌握各个知识点是解题的关键.
【题型】解答题
【结束】
18
【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(
(3)99991×99999=___________________(直接填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、 D. 求证:PC=PD.

查看答案和解析>>
科目:初中数学 来源: 题型:
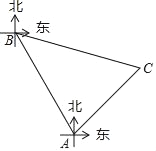
【题目】黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船沿北偏西30°方向航行60海里后到达B处,此时测得该目标C在它的南偏东75方向,求此时该船与目标C之间的距离CB的长度,(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com