
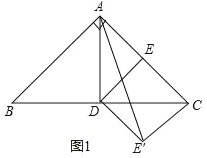
【题目】在等腰直角三角形ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD.
(1)如图1,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当AD=![]() 时,求AE的值.
时,求AE的值.
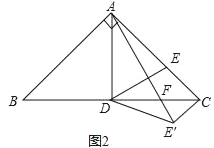
(2)如图2,在AC上取一点E,使得CE=![]() AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.
AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)已知BAC=90°,AB=AC,D是斜边BC的中点,可得∠ADC=90°,∠ACD=45°,在Rt△ADC中,求得AC=2![]() ,即可求得CE =
,即可求得CE =![]() ,根据翻折可得CE=CE'=
,根据翻折可得CE=CE'=![]() ,∠ACE'=90°,由勾股定理即可求得AE的长;(2)过B作AE’的垂线交AD于点G,交AC于点H,易证△ABH≌△CAE',根据全等三角形的性质可得AH=CE’=CE,再证明△ABG≌△CAF,即可得AG=CF,再证明CF=
,∠ACE'=90°,由勾股定理即可求得AE的长;(2)过B作AE’的垂线交AD于点G,交AC于点H,易证△ABH≌△CAE',根据全等三角形的性质可得AH=CE’=CE,再证明△ABG≌△CAF,即可得AG=CF,再证明CF=![]() AD=
AD=![]() CD,所有DF=CF.
CD,所有DF=CF.
试题解析:
(1)∵∠BAC=90°,AB=AC,D是斜边BC的中点,
∴∠ADC=90°,∠ACD=45°,
在Rt△ADC中,AC=AD×sin45°=2![]() ,
,
∵E是AC的中点,
∴CE=![]() AC=
AC=![]() ,
,
∵将△CDE沿CD翻折到△CDE',
∴CE=CE'=![]() ,∠ACE'=90°,
,∠ACE'=90°,
由勾股定理得:AE=![]() =
=![]() ;
;
(2)证明:过B作AE’的垂线交AD于点G,交AC于点H,
∵∠ABH+∠BAF=90°,∠CAF+∠BAF=90°,
∴∠ABH=∠CAF,
又∵AB=AC,∠BAH=∠ACE’=90°,
∴△ABH≌△CAE',
∴AH=CE’=CE,
∵CE=![]() AC,
AC,
∴AH=HE=CE,
∵D是BC中点,
∴DE是△BCH的中位线,
∴DE∥BH,
∴G是AD中点,
∵在△ABG和△CAF中,AB=AC,∠BAD=∠ACD=45°,∠ABH=∠CAF,
∴△ABG≌△CAF,
∴AG=CF,
∵AG=![]() AD,
AD,
∴CF=![]() AD=
AD=![]() CD,
CD,
∴DF=CF.


科目:初中数学 来源: 题型:
【题目】手工拉面是我国的传统美食.已知1根面条拉扣1次成2根.拉扣2次就成2x2根……每拉扣1次,面条数就增加1倍.
(1)设2位师傅各拿1根面条分别拉扣3次所成面条数之和为![]() ,3位师傅各拿1根面条分别拉扣2次所成面条数之和为
,3位师傅各拿1根面条分别拉扣2次所成面条数之和为![]() .试通过计算比较
.试通过计算比较![]() 的大小;
的大小;
(2)设张师傅在某次拉扣后所成面条的长度为0.8米/根,总长度为![]() 米,如果他又拉扣了2次,求此时面条增加了多少根?
米,如果他又拉扣了2次,求此时面条增加了多少根?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:圆是最完美的图形,它具有一些特殊的性质:同弧或等弧所对的圆周角相等,一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”,再利用圆的性质将问题进行转化,往往能化隐为显、化难为易。
解决问题:如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.
(1)使∠APB=30°的点P有_______个;
(2)若点P在y轴正半轴上,且∠APB=30°,求满足条件的点P的坐标;
(3)设sin∠APB=m,若点P在y轴上移动时, 满足条件的点P有4个,求m的取值范围.
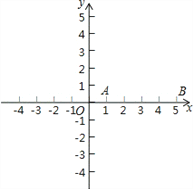
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).
(1)请按下列要求画图:
①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2.
(2)若将△A1B1C1绕点M旋转可得到△A2B2C2,请直接写出旋转中心M点的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼身体,强健体魄,小明和小强约定每天在两家之间往返长跑20分钟. 两家正好在同一直线道路边上,某天小明和小强从各自的家门口同时出发,沿两家之间的直线道路按各自的速度匀速往返跑步,已知小明的速度大于小强的速度. 在跑步的过程中,小明和小强两人之间的距离y(米)与他们出发的时间x(分钟)之间的关系如图所示,在他们3次相遇中,离小明家最近那次相遇时距小明家____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )
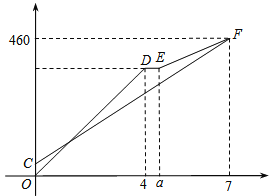
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个两位数A,十位数字为a,个位数字为b,交换a和b的位置,得到一个新的两位数B,则A+B一定能被______整除,A-B一定能被______整除;
(2)一个三位数M,百位数字为a,十位数字为b,个位数字为c(a,b,c均为1至9的整数),交换a和c的位置,得到一个新的三位数N.请用含a、b、c的式子分别表示数N与M-N;
(3) 若(2)中a比b大1,M比N大792,求M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com