
【题目】
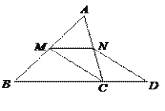
已知:如图,在△ABC中,M是边AB的中点,D是边BC延长线上一点,![]() ,DN∥CM,交边AC于点N.
,DN∥CM,交边AC于点N.
(1)求证:MN∥BC;
(2)当∠ACB为何值时,四边形BDNM是等腰梯形?并证明你的猜想.
【答案】(1)见解析;
(2)当∠ACB=90°时,四边形BDNM是等腰梯形.
证明见解析.
【解析】
(1)证法一:取边BC的中点E,联结ME.
∵BM=AM,BE=EC,∴ME∥AC.
∴∠MEC=∠NCD.
∵![]() ,∴
,∴![]() .
.
∵DN∥CM,∴∠MCE=∠D.
∴△MEC≌△NCD.
∴![]() .
.
又∵CM∥DN,∴四边形MCDN是平行四边形.
∴MN∥BC.
证法二:延长CD到F,使得![]() ,联结AF.
,联结AF.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,∴MC∥AF.
,∴MC∥AF.
∵MC∥DN,∴ND∥AF.
又∵![]() ,∴
,∴![]() .
.
∴MN∥BC.
(2)解:当∠ACB=90°时,四边形BDNM是等腰梯形.
证明如下:
∵MN∥BD,BM与DN不平行,∴四边形BDNM是梯形.
∵∠ACB=90°,![]() ,∴
,∴![]() .
.
∵![]() ,∴BM
,∴BM![]() DN.
DN.
∴四边形BDNM是等腰梯形.


科目:初中数学 来源: 题型:
【题目】甲骑电动车、乙骑摩托车都从M地出发,沿一条笔直的公路匀速前往N地,甲先出发一段时间后乙再出发,甲、乙两人到达N地后均停止骑行.已知M、N两地相距![]() km,设甲行驶的时间为x(h),甲、乙两人之间的距离为y(km),表示y与x函数关系的部分图象如图所示.请你解决以下问题:
km,设甲行驶的时间为x(h),甲、乙两人之间的距离为y(km),表示y与x函数关系的部分图象如图所示.请你解决以下问题:

(1)求线段BC所在直线的函数表达式;
(2)求点A的坐标,并说明点A的实际意义;
(3)根据题目信息补全函数图象.(须标明相关数据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了![]() 市
市![]() 户居民全年月平均用电量(单位:千瓦时)数据如下:
户居民全年月平均用电量(单位:千瓦时)数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表:
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
| ||
| ||
|
| |
|
| |
|
| |
合计 |
|
|
画出频数分布直方图,如下:

(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图,则不低于![]() 千瓦时的部分圆心角的度数为_____________;
千瓦时的部分圆心角的度数为_____________;
(3)若![]() 市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图,A.B.C为数轴上三点,若点C到A的距离是点C到B的距离的2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为-1,点B表示的数为2.表示数1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示数0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

(1)数 所表示的点是(M,N)的好点;
(2)现有一只电子蚂蚁P从点N出发,以每秒2个单位的速度沿数轴向左运动,运动时间为t.当t为何值时,P、M、N中恰有一个点为其余两点的好点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学解方程的过程,请仔细阅读,并解答所提出的问题.
![]()
解:去分母,得![]() ,①
,①
去括号,得![]() ,②
,②
移项,得![]() ,③
,③
合并同类项,得![]() ,④
,④
系数化为![]() ,得
,得![]() .⑤
.⑤
(1)聪明的你知道小明的解答过程在________(填序号)处出现了错误,出现错误的原因是违背了__________.
A.等式的基本性质![]() ;B.等式的基本性质
;B.等式的基本性质![]() ;C.去括号法则;D加法交换律.
;C.去括号法则;D加法交换律.
(2)请你写出正确的解答过程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学学生在学习等腰三角形性质“三线合一”时
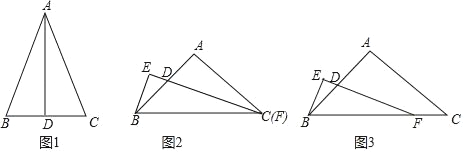
(1)(探究发现)如图1,在△ABC中,若AD平分∠BAC,AD⊥BC时,可以得出AB=AC,D为BC中点,请用所学知识证明此结论.
(2)(学以致用)如果Rt△BEF和等腰Rt△ABC有一个公共的顶点B,如图2,若顶点C与顶点F也重合,且∠BFE=![]() ∠ACB,试探究线段BE和FD的数量关系,并证明.
∠ACB,试探究线段BE和FD的数量关系,并证明.
(3)(拓展应用)如图3,若顶点C与顶点F不重合,但是∠BFE=![]() ∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=![]() AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com