
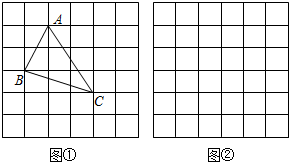
���� ��1�����á�ABC���ھ��������ȥ��Χ��������������ó��𰸣�
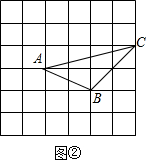
��2�����á�ABC���ھ��������ȥ��Χ��������������ó��𰸣�
��� 
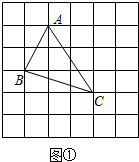 �⣺��1����ͼ����ʾ����ABC�����Ϊ��3��3-$\frac{1}{2}$��1��2-$\frac{1}{2}$��2��3-$\frac{1}{2}$��1��3=3.5��
�⣺��1����ͼ����ʾ����ABC�����Ϊ��3��3-$\frac{1}{2}$��1��2-$\frac{1}{2}$��2��3-$\frac{1}{2}$��1��3=3.5��
�ʴ�Ϊ��3.5��
��2����ͼ����ʾ��
2��4-$\frac{1}{2}$��1��4-$\frac{1}{2}$��1��2-$\frac{1}{2}$��2��2
=3��
���� ������Ҫ�����˹��ɶ����Լ����������������������ȷ������ABC�ǽ���ؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
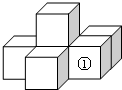 ��ͼ����6��ͬ����С��������ڳɵļ����壮������������ߺ����ü����������������״ͼ��˵����ȷ���ǣ�������
��ͼ����6��ͬ����С��������ڳɵļ����壮������������ߺ����ü����������������״ͼ��˵����ȷ���ǣ�������| A�� | �����濴�ı䣬�����濴�ı� | B�� | �����濴���䣬�����濴���� | ||
| C�� | �����濴���䣬�����濴���� | D�� | �����濴�ı䣬�����濴���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
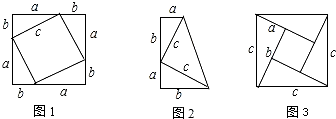
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
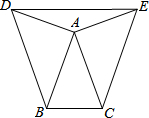 ��ͼ����֪AD=AE����BDE=��CED����ABD=��ACE��
��ͼ����֪AD=AE����BDE=��CED����ABD=��ACE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��4�� | B�� | ��-3��3�� | C�� | ��3��-4�� | D�� | ��-3��-4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com