
 如图,△ABC为等腰直角三角形,∠BAC=90°,在边BC上取点D,使BD=2DC,BE⊥AD交AC于E,垂足为F.求证:AE=EC.
如图,△ABC为等腰直角三角形,∠BAC=90°,在边BC上取点D,使BD=2DC,BE⊥AD交AC于E,垂足为F.求证:AE=EC.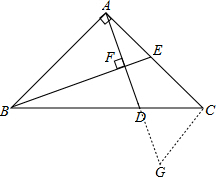 证明:作AC⊥CG交AD的延长线于点G,
证明:作AC⊥CG交AD的延长线于点G,
|
| AB |
| CG |
| BD |
| CD |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
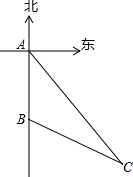 某次台风袭击了我国西南部海域.如图,台风来临前,我国海上搜救中心A接到一渔船遇险的报警,于是令位于A的正南方向180海里的救援队B立即施救.已知渔船所处位置C在A的南偏东34°方向,在B的南偏东63°方向,此时离台风来到C处还有12小时,如果救援船每小时行驶20海里,试问能否在台风来到之前赶到C处对其施救?
某次台风袭击了我国西南部海域.如图,台风来临前,我国海上搜救中心A接到一渔船遇险的报警,于是令位于A的正南方向180海里的救援队B立即施救.已知渔船所处位置C在A的南偏东34°方向,在B的南偏东63°方向,此时离台风来到C处还有12小时,如果救援船每小时行驶20海里,试问能否在台风来到之前赶到C处对其施救?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
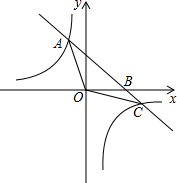 如图,已知直线y=-x+4与反比例函数y=
如图,已知直线y=-x+4与反比例函数y=| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com