
���� ��1���ɡ�ONP=��M����NOP=��MON���ó���NOP�ס�MON��֤����P�ǡ�MON�������Ƶ㣻��P��PD��x����D����tan��POD=$\frac{MN}{ON}=\sqrt{3}$�������AON=60�㣬�ɵ�M��N������ó���MNO=90�㣬�����������ε����ʵó���NPO=��MNO=90�㣬��Rt��OPN�У������Ǻ������OP=$\frac{\sqrt{3}}{2}$��OD=$\frac{\sqrt{3}}{4}$��PD=$\frac{3}{4}$�����ɵó��𰸣�
��2����MH��x����H���ɹ��ɶ������OM=2$\sqrt{3}$��ֱ��OM�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x��ON=2����MOH=30�㣬���������������PQ��x����Q�������Ƶ�����ʵó�PO=PN��OQ=$\frac{1}{2}$ON=1�����P�������꼴�ɣ�
�����MN=$\sqrt{��\sqrt{3}��^{2}+{1}^{2}}$=2�������������ε����ʵó�$\frac{PN}{ON}=\frac{MN}{MO}$�����PN=$\frac{2\sqrt{3}}{3}$�������P�ĺ����꼴�ɣ�
��3��֤��OM=2$\sqrt{3}$=ON����MON=60�㣬�ó���MON�ǵȱ������Σ��ɵ�P�ڡ�MON���ڲ����ó���PON�١�OMN����PNO�١�MON�����ɵó����ۣ�
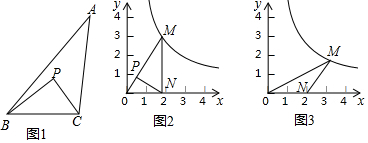
��� �⣺��1���ߡ�ONP=��M����NOP=��MON��
���NOP�ס�MON��
���P�ǡ�MON�������Ƶ㣻
��P��PD��x����D����tan��POD=$\frac{MN}{ON}=\sqrt{3}$��
���AON=60�㣬
�ߵ���M�������ǣ�$\sqrt{3}$��3������N�������ǣ�$\sqrt{3}$��0����
���MNO=90�㣬
�ߡ�NOP�ס�MON��
���NPO=��MNO=90�㣬
��Rt��OPN��OP=ONcos60��=$\frac{\sqrt{3}}{2}$��
��OD=OPcos60��=$\frac{\sqrt{3}}{2}$��$\frac{1}{2}$=$\frac{\sqrt{3}}{4}$��PD=OP•sin60��=$\frac{\sqrt{3}}{2}$��$\frac{\sqrt{3}}{2}$=$\frac{3}{4}$��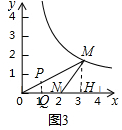
��P��$\frac{\sqrt{3}}{4}$��$\frac{3}{4}$����
��2����MH��x����H����ͼ3��ʾ��
�ߵ�M�������ǣ�3��$\sqrt{3}$������N�������ǣ�2��0����
��OM=$\sqrt{{3}^{2}+��\sqrt{3}��^{2}}$=2$\sqrt{3}$��ֱ��OM�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x��ON=2����MOH=30�㣬
�����������
����ͼ3��ʾ����P�ǡ�MON�����Ƶ㣬
���PON�ס�NOM����PQ��x����Q��
��PO=PN��OQ=$\frac{1}{2}$ON=1��
��P�ĺ�����Ϊ1��
��y=$\frac{\sqrt{3}}{3}$��1=$\frac{\sqrt{3}}{3}$��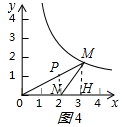
��P��1��$\frac{\sqrt{3}}{3}$����
����ͼ4��ʾ��
�ɹ��ɶ����ã�MN=$\sqrt{��\sqrt{3}��^{2}+{1}^{2}}$=2��
��P�ǡ�MON�����Ƶ㣬
���PNM�ס�NOM��
��$\frac{PN}{ON}=\frac{MN}{MO}$����$\frac{PN}{2}=\frac{2}{2\sqrt{3}}$��
��ã�PN=$\frac{2\sqrt{3}}{3}$��
��P��������Ϊ$\frac{2\sqrt{3}}{3}$������y=$\frac{\sqrt{3}}{3}$�ã�$\frac{2\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$x��
��ã�x=2��
��P��2��$\frac{2\sqrt{3}}{3}$����
������������MON�������Ƶ������Ϊ��1��$\frac{\sqrt{3}}{3}$����2��$\frac{2\sqrt{3}}{3}$����
��3�����ڵ�M�͵�N��ʹ��MON�������Ƶ㣬M��$\sqrt{3}$��3����N��2$\sqrt{3}$��0�����������£�
��M��$\sqrt{3}$��3����N��2$\sqrt{3}$��0����
��OM=2$\sqrt{3}$=ON����MON=60�㣬
���MON�ǵȱ������Σ�
�ߵ�P�ڡ�MON���ڲ���
���PON�١�OMN����PNO�١�MON��
����ڵ�M�͵�N��ʹ��MON�������Ƶ㣮
���� �����Ƿ����������ۺ���Ŀ�����������������ε����ʡ����Ƶ���ж������ʡ����Ǻ�����������ͼ�����ʡ����ɶ������ȱ������ε��ж������ʡ�ֱ�߽���ʽ��ȷ����֪ʶ�������ۺ���ǿ����һ���Ѷȣ������������Ƶ���ж��������ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
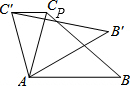 ��ͼ���ڡ�ABC�У���CAB=78�㣬��ͬһƽ���ڣ�����ABC�Ƶ�A��ת����AB��C���λ�ã�ʹ��CC���AB��BC��B��C�佻�ڵ�P�����BPB��Ĵ�СΪ24�㣮
��ͼ���ڡ�ABC�У���CAB=78�㣬��ͬһƽ���ڣ�����ABC�Ƶ�A��ת����AB��C���λ�ã�ʹ��CC���AB��BC��B��C�佻�ڵ�P�����BPB��Ĵ�СΪ24�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ����ȷ���Ҵ��� | B�� | ����ȷ���״��� | C�� | �ס��Ҿ���ȷ | D�� | �ס��Ҿ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
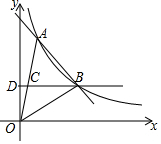 ��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{a}{x}$��ͼ���ڵ�һ������A��B���㣬B�������Ϊ��3��2��������OA��OB����B��BD��y�ᣬ����ΪD����OA��C����OC=CA��
��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{a}{x}$��ͼ���ڵ�һ������A��B���㣬B�������Ϊ��3��2��������OA��OB����B��BD��y�ᣬ����ΪD����OA��C����OC=CA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����BAC��ƽ���߽���ABC�����Բ�ڵ�D����ABC��ƽ���߽�AD�ڵ�E��
��ͼ����BAC��ƽ���߽���ABC�����Բ�ڵ�D����ABC��ƽ���߽�AD�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
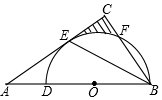 ��ͼ���ڡ�ABC�У�BE�����Ľ�ƽ���ߣ���C=90�㣬D��AB���ϣ���DBΪֱ���İ�ԲO������E����BC�ڵ�F��
��ͼ���ڡ�ABC�У�BE�����Ľ�ƽ���ߣ���C=90�㣬D��AB���ϣ���DBΪֱ���İ�ԲO������E����BC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
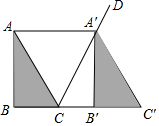 ��ͼ������ABC��������BC����ƽ������A'B'C'��ʹ��A'���ڡ�ACB�����ƽ����CD�ϣ�����AA'��
��ͼ������ABC��������BC����ƽ������A'B'C'��ʹ��A'���ڡ�ACB�����ƽ����CD�ϣ�����AA'���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com