
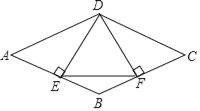
【题目】如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DE⊥BC于点F,连接EF,求证:
(1)△ADE≌△CDF;
(2)若∠A=60°,AD=4,求△EDF的周长.
【答案】(1)见解析;(2)6![]()
【解析】
(1)利用菱形的性质得到AD=CD,∠A=∠C,进而利用AAS证明两三角形全等;
(2)由△ADE≌△CDF得到DE=DF,进而证明出△DEF是等边三角形,再解直角三角形求出DF的长,即可求出△EDF的周长.
(1)∵四边形ABCD是菱形,
∴AD=CD,∠A=∠C,
∵DE⊥BA,DF⊥CB,
∴∠AED=∠CFD=90°,
在△ADE和△CDF,
∵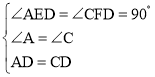 ,
,
∴△ADE≌△CDF;
(2)∵△ADE≌△CDF,
∴DE=DF,∠ADE=∠CDF,
∵菱形ABCD,DE⊥AB于点E,∠A=60°,
∴∠ADC=120°,∠ADE=30°,
∴∠EDF=60°,
∴△DEF是等边三角形,
在Rt△AED中,∵AD=4,∠A=60°,
∴DE=sin60°AD=2![]() ,
,
∴△EDF的周长=3DE=6![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3经过点A(1,0)和点B(5,0).
(1)求该抛物线所对应的函数解析式;
(2)该抛物线与直线![]() 相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.
相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.
①连结PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
②连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.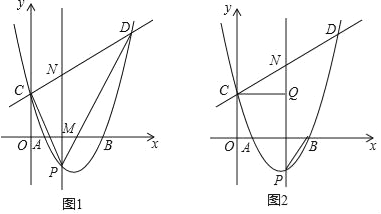
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是必然事件的是( )
A. 掷一次骰子,向上一面的点数是6B. 经过有交通信号灯的路口,遇到红灯
C. 任意画一个三角形,其内角和是![]() D. 射击运动员射击一次,命中靶心
D. 射击运动员射击一次,命中靶心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
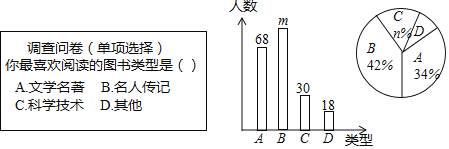
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
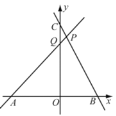
【题目】如图,在平面直角坐标系xOy中,已知直线PA是一次函数![]() 的图象,直线PB是一次函数
的图象,直线PB是一次函数![]() 的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.若四边形PQOB的面积是5.5,且
的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.若四边形PQOB的面积是5.5,且![]() ,若存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,则点D的坐标为________.
,若存在一点D,使以A、B、P、D为顶点的四边形是平行四边形,则点D的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.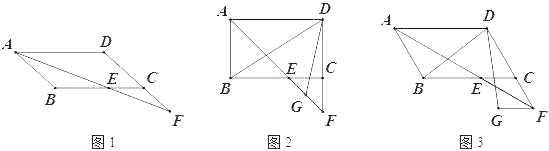
查看答案和解析>>
科目:初中数学 来源: 题型:
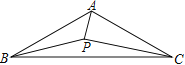
【题目】如图,△ABC中,AB=AC,点P为△ABC内一点,∠APB=∠BAC=120°.若AP+BP=4,则PC的最小值为( )
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下:

根据所给信息,解决下列问题:
(1)a= ,b= ;
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com