
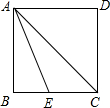
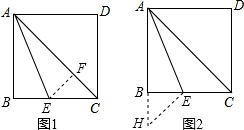
 如图,已知:正方形ABCD中,∠BAC的平分线交BC于E,求证:AB+BE=AC.
如图,已知:正方形ABCD中,∠BAC的平分线交BC于E,求证:AB+BE=AC.
|
|


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
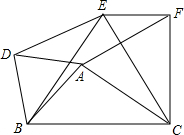 如图,以△ABC的三边为边在BC同一侧分别作三个等边三角形△ABD、△BCE、△ACF.
如图,以△ABC的三边为边在BC同一侧分别作三个等边三角形△ABD、△BCE、△ACF.查看答案和解析>>
科目:初中数学 来源: 题型:
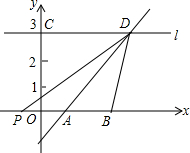 如图,在直角坐标平面内,直线y=x-1与x轴交于点A,过点C(0,3)的直线l∥x轴,与直线y=x-1交于点D,点P从原点O出发沿x轴负半轴移动,连接PD,设点P移动的距离为m.
如图,在直角坐标平面内,直线y=x-1与x轴交于点A,过点C(0,3)的直线l∥x轴,与直线y=x-1交于点D,点P从原点O出发沿x轴负半轴移动,连接PD,设点P移动的距离为m.查看答案和解析>>
科目:初中数学 来源: 题型:
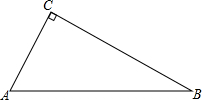 如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )
如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )| A、20 | ||
| B、10 | ||
C、10
| ||
D、20
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图①,图②,图③…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第20个“广”字中的棋子个数是( )
如图①,图②,图③…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第20个“广”字中的棋子个数是( )| A、43 | B、44 | C、45 | D、46 |
查看答案和解析>>
科目:初中数学 来源: 题型:
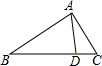 如图,点D是△ABC的边BC上一点,能判断△ACD∽BCA的条件是( )
如图,点D是△ABC的边BC上一点,能判断△ACD∽BCA的条件是( )| A、AC2=BC•DC |
| B、AC•AD=BC•AB |
| C、∠CAD=∠BAD |
| D、∠C=∠B |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com