
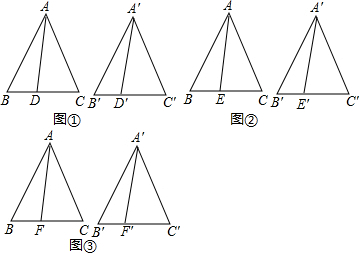
分析 (1)首先由△ABC≌△A′B′C′,根据全等三角形的性质得出AB=A′B′,∠B=∠B′,BC=B′C′,再由中线的定义可得BD=B′D′,再利用ASA定理证明△ABD≌△A′B′D′可得AD=A′D′;
(2)首先由△ABC≌△A′B′C′,根据全等三角形的性质得出AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′,再由高线的定义可得∠BAE=∠B′A′E′,再利用ASA定理证明△ABE≌△A′B′E′可得AE=A′E′.
(3)首先由△ABC≌△A′B′C′,根据全等三角形的性质得出AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′,再由角平分线的定义可得∠BAF=∠B′A′F′,再利用ASA定理证明△ABF≌△A′B′F′可得AF=A′F′.
解答 证明:(1)∵△ABC≌△A′B′C′,
∴AB=A′B′,∠B=∠B′,BC=B′C′
∵AD和A′D′分别是△ABC和△A′B′C′的中线,
∴BD=$\frac{1}{2}$BC,B′D′=$\frac{1}{2}$B′C′,
∴BD=B′D′.
在△ABD和△A′B′D′中,$\left\{\begin{array}{l}{AB=A′B′}\\{∠B=∠B′}\\{BD=B′D′}\end{array}\right.$,
∴△ABD≌△A′B′D′(ASA),
∴AD=A′D′;
(2)证明:∵△ABC≌△A′B′C′,
∴AB=A′B′,∠B=∠B′,
∵AE,A′E′分别是△ABC和△A′B′C′的对应高线,
∴∠BEA=90°,∠B′E′A′=90°,
∴∠BDA=∠B′D′A′.
在△ABE和△A′B′E′中,
$\left\{\begin{array}{l}{∠BEA=∠B′E′A′}\\{∠B=∠B′}\\{AB=A′B′}\end{array}\right.$,
∴△ABE≌△A′B′E′(ASA),
∴AE=A′E′.
(3)证明:∵△ABC≌△A′B′C′,
∴AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′,
∵AF和A′F′分别是△ABC和△A′B′C′的角平分线,
∴∠BAF=$\frac{1}{2}$∠BAC,∠B′A′F′=$\frac{1}{2}$∠B′A′C′,
∴∠BAF=∠B′A′F′.
在△ABF和△A′B′F′中,$\left\{\begin{array}{l}{∠BAF=∠B′A′F′}\\{AB=A′B′}\\{∠B=∠B′}\end{array}\right.$,
∴△ABF≌△A′B′F′(ASA),
∴AF=A′F′.
点评 此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定方法:SSS、SAS、ASA、AAS、HL.根据全等三角形的对应边相等、对应角相等得出AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′是解题的关键.


科目:初中数学 来源: 题型:解答题
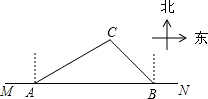 2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?
2009年3月21日邵阳市荣获“省卫生城市称号”,在创卫过程中,要在东西方向M、N两地之间修建一条道路,已知:如图,C点周围180米范围内为文物保护区,在MN上点A处测得C在A的北偏东60°方向上,从A向东走500米到达B处,测得C在B的北偏西45°方向上,问MN是否穿过文物保护区?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
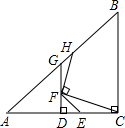 如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.
如图,CE=GF,AC=BC,∠ACB=90°,D是中点,DG⊥AC,FH⊥FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
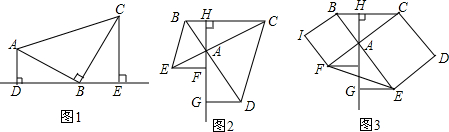
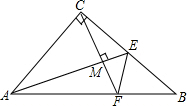 如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:
如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | B. | a8÷a4=a2 | C. | (a-b)2=a2-b2 | D. | 3m+4n=7mn |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com