
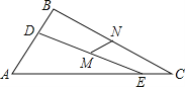
【题目】 如图,△ABC中,∠A=60°,AC>AB>2,点D,E分别在边AB,AC上,且BD=CE=2,连接DE,点M是DE的中点,点N是BC的中点,线段MN的长为______.
【答案】![]()
【解析】
如图,作CH∥AB,连接DN,延长DN交CH于H,连接EH,作CJ⊥EH于J.首先证明CH=EC,∠ECH=120°,解直角三角形求出EH,利用三角形中位线定理即可解决问题.
解:如图,作CH∥AB,连接DN,延长DN交CH于H,连接EH,作CJ⊥EH于J.
∵BD∥CH,
∴∠B=∠NCH,
∵BN=CN,∠DNB=∠KNC,
∵△DNB≌△HNC(ASA),
∴BD=CH,DN=NH,
∵BD=EC=2,
∴EC=CH=2,
∵∠A+∠ACH=180°,∠A=60°,
∴∠ECH=120°,
∵CJ⊥EH,
∴EJ=JH=ECcos30°=![]() ,
,
∴EH=2EJ=2![]() ,
,
∵DM=ME,DN=NH,
∴MN=![]() EH=
EH=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
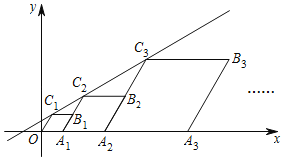
【题目】如图,在平面直角坐标系中,四边形OA1B1C1,A1A2B2C2,A2A3B3C3,…都是菱形,点A1,A2,A3,…都在x轴上,点C1,C2,C3,…都在直线y=![]() x+
x+![]() 上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是__.
上,且∠C1OA1=∠C2A1A2=∠C3A2A3=…=60°,OA1=1,则点C6的坐标是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动,当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒.
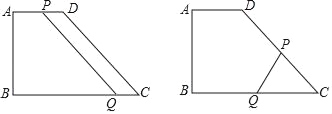
(1)当t为多少秒时,四边形PQCD是平行四边形?请说明理由;
(2)当t为多少秒时,AQ=DC?请说明理由;
(3)当t为多少秒时,PQ⊥DC?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,当α=0°时,正方形ABCD与正方形AEFG互相重合,现将正方形AEFG绕点A逆时针旋转,当α=_____时(0°<α<360°),正方形AEFG的顶点F会落在正方形ABCD的两对角线AC或BD所在直线上.
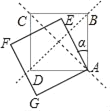
查看答案和解析>>
科目:初中数学 来源: 题型:
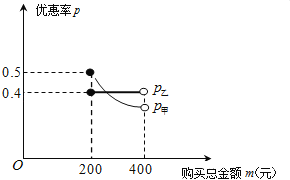
【题目】元旦期间,甲、乙两家商场都进行了促销活动,如何才能更好地衡量钏销对消费者受益程度的大小呢?某数学小组通过合作探究发现用优惠率p=![]() (其中k代表优惠金额,m代表顾客购买商品的总金额)可以很好地进行衡量,优惠率p越大,消费者受益程度越大;反之就越小.经统计,若顾客在甲、乙两家商场购买商品的总金额都为m(200≤m<400)元时,优惠率分别为P甲=
(其中k代表优惠金额,m代表顾客购买商品的总金额)可以很好地进行衡量,优惠率p越大,消费者受益程度越大;反之就越小.经统计,若顾客在甲、乙两家商场购买商品的总金额都为m(200≤m<400)元时,优惠率分别为P甲=![]() 与P乙=
与P乙=![]() ,它们与m的关系图象如图所示,其中p甲与m成反比例函数关系,p乙保持定值.
,它们与m的关系图象如图所示,其中p甲与m成反比例函数关系,p乙保持定值.
(1)求出k甲的值,并用含m的代数式表示k乙.
(2)当购买总金额m(元)在200≤m<400的条件下时,指出甲、乙两家商场正在采取的促销方案分别是什么.
(3)品牌、质量、规格等都相同的基本种商品,在甲、乙两家商场的标价都是m(200≤m<400)元,你认为选择哪家商场购买该商品花钱少些?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,∠ACB=90°,AC=4,BC=6,点E,F分别在边AB,BC上,将△ABC沿直线EF折叠,点B恰好落在AC边上的点D处,且CD=3.
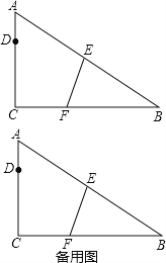
(1)求CF的长;
(2)点G是射线BA上的一个动点,连接DG,GC,BD,△DGC的面积与△DGB的面积相等,
①当点G在线段BA上时,求BG的长;
②当点G在线段BA的延长线上时,BG=______;
(3)将直线EF平移,平移后的直线与直线BC,直线AC分别交于点M和点N,以线段MN为一边作正方形MNPQ,点P与点B在直线MN两侧,连接PD,当PD∥BC时,请直接写出tan∠QBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班到毕业时共结余班费1800元,班委会决定拿出一部分钱为老师购买纪念品,其余用于毕业晚会上给全班50位同学每人购买一件文化衫或者一本留言册作为纪念,了解到每件文化衫比每本留言册多8元,用200元恰好能购买4件文化衫和2本留言册.
(1)求买一件文化衫、一本留言册各需多少元?
(2)如果用于给老师买纪念品的钱数不少于120元,则这50件纪念品(每人一件文化衫或一本留言册)中最多能买多少件文化衫?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AB∥CD,∠DAB=90°,AD=4,AB=2CD=6,E是边BC上一点,过点D、E分别作BC、CD的平行线交于点F,联结AF并延长,与射线DC交于点G.
(1)当点G与点C重合时,求CE:BE的值;
(2)当点G在边CD上时,设CE=m,求△DFG的面积;(用含m的代数式表示)
(3)当△AFD∽△ADG时,求∠DAG的余弦值.
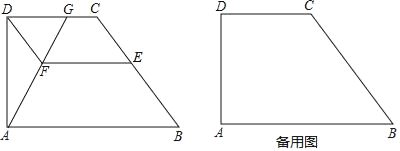
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“促民生、促经济”政策,某市玻璃制品销售公司今年1月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售的件数).下表是甲、乙两位职工今年四月份的工资情况信息:
职工 | 甲 | 乙 |
月销售件数/件 | 200 | 180 |
月工资/元 | 1800 | 1700 |
试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com