
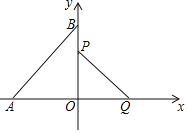
【题目】如图,在直角坐标系中,点A、B分别在x轴和y轴上,△OBA是等腰直角三角形且AB=![]() ,线段PQ=1,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动.
,线段PQ=1,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动.
(1)求A、B两点的坐标;
(2)若P运动的路程为m,△OPA的面积为S,求S与m之间的函数关系式;
(3)当点P运动一周时,点Q运动的总路程为______.
【答案】(1)A点的坐标为:(-1,0),B点的坐标为:(0,1);(2)S与m之间的函数关系式为S=![]() m(0<m≤1),或S=
m(0<m≤1),或S=![]() +
+![]() -
-![]() m(1<m<
m(1<m<![]() +1);(3)2
+1);(3)2![]() .
.
【解析】
(1)由△OBA是等腰直角三角形且AB=![]() ,得出OA=OB=1,即可得出A、B两点的坐标;(2)分三种情况讨论:①当点P在OB边上时,由三角形面积公式即可得出结果;②当点P在AB边上时,作PD⊥OA于D,△APD是等腰直角三角形,则PB=m-1,求出AP的长,由等腰直角三角形的性质得出PD的长,由三角形面积公式即可得出结果;③当点P在AO边上时,△OPA不存在;(3)根据题意正确画出从O→B→A运动一周的图形,分四种情况进行计算:①点P从O→B时,路程是线段PQ的长;②当点P从B→C时(QC⊥AB,C为垂足),点Q从O运动到Q,计算OQ的长就是运动的路程;③点P从C→A时,点Q由O向左运动,路程为QO;④点P从A→O时,点Q运动的路程就是点P运动的路程;最后相加即可.
,得出OA=OB=1,即可得出A、B两点的坐标;(2)分三种情况讨论:①当点P在OB边上时,由三角形面积公式即可得出结果;②当点P在AB边上时,作PD⊥OA于D,△APD是等腰直角三角形,则PB=m-1,求出AP的长,由等腰直角三角形的性质得出PD的长,由三角形面积公式即可得出结果;③当点P在AO边上时,△OPA不存在;(3)根据题意正确画出从O→B→A运动一周的图形,分四种情况进行计算:①点P从O→B时,路程是线段PQ的长;②当点P从B→C时(QC⊥AB,C为垂足),点Q从O运动到Q,计算OQ的长就是运动的路程;③点P从C→A时,点Q由O向左运动,路程为QO;④点P从A→O时,点Q运动的路程就是点P运动的路程;最后相加即可.
(1)∵△OBA是等腰直角三角形且AB=![]() ,
,
∴OA=OB=1,
∴A点的坐标为:(-1,0),B点的坐标为:(0,1);
(2)分三种情况讨论:
①当点P在OB边上,即0<m≤1时,如图1所示:
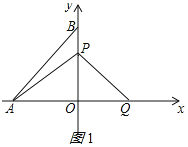
△OPA的面积S=![]() OA×OP=
OA×OP=![]() ×1×m=
×1×m=![]() m;
m;
②当点P在AB边上,即1<m<![]() +1时,如图2所示:
+1时,如图2所示:
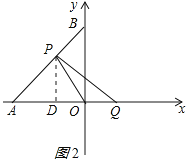
作PD⊥OA于D,△APD是等腰直角三角形,
∵PB=m-1,
∴AP=AB-PB=![]() -(m-1)=
-(m-1)=![]() +1-m,
+1-m,
∴PD=![]() AP=
AP=![]() (
(![]() +1-m)=1+
+1-m)=1+![]() -
-![]() m,
m,
∴△OPA的面积=![]() OA×PD=
OA×PD=![]() ×1×(1+
×1×(1+![]() -
-![]() m)=
m)= ![]() +
+![]() -
-![]() m,即S=
m,即S=![]() +
+![]() -
-![]() m;
m;
③当点P在AO边上,即![]() +1≤m≤
+1≤m≤![]() +2时,△OPA不存在;
+2时,△OPA不存在;
综上所述,S与m之间的函数关系式为S=![]() m(0<m≤1),或S=
m(0<m≤1),或S=![]() +
+![]() -
-![]() m(1<m<
m(1<m<![]() +1);
+1);
(3)∵△OBA是等腰直角三角形,
∴∠ABO=∠BAO=45°,
∵OA=OB=1,PQ=1,
①当点P从O→B时,点Q运动的路程为PQ的长,即为1;
②如图3所示,QC⊥AB,则∠ACQ=90°,即PQ运动到与AB垂直时,垂足为P,
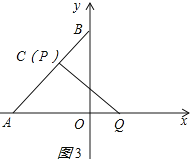
当点P从B→C时,
∵∠ABO=∠BAO=45°,
∴∠OQC=90°-45°=45°,
∴AQ=![]() PQ=
PQ=![]() ,
,
∴OQ=AQ-OA=![]() -1,
-1,
则点Q运动的路程为QO=![]() -1;
-1;
③当点P从C→A时,点Q运动的路程为QO=![]() -1;
-1;
④当点P从A→O时,点Q运动的路程为AO=1,
∴点Q运动的总路程为:1+![]() -1+
-1+![]() -1+1=2
-1+1=2![]() ;
;
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】★若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似.如图,如果扇形AOB与扇形A1O1B1是相似扇形,且半径OA∶O1A1=k(k为不等于0的常数).那么下面四个结论:①∠AOB=∠A1O1B1;②△AOB∽△A1O1B1;③![]() =k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )
=k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的一种图形的名称 ;
(2)如图 1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB 为勾股边且有对角线相等的勾股四边形 OAMB 的顶点M 的坐标: ;
(3)如图 2,将△ABC 绕顶点 B 按顺时针方向旋转 60°,得到△DBE,连接 AD、DC,∠DCB=30°.求证: DC2 BC2 AC2 ,即四边形 ABCD 是勾股四边形;
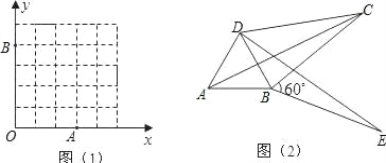
(4)若将图 2 中△ABC 绕顶点 B 按顺时针方向旋转 a 度(0°<a <90°),得到△DBE,连接 AD、DC,则当∠DCB= °时,四边形BECD 是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成如下图所示统计图:
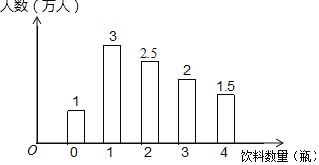
(1)在A出口的被调查游客中,购买瓶装饮料的数量的中位数是______瓶、众数是______瓶、平均数是______瓶;
(2)已知A、B、C三个出口的游客量比为2:2:1,用上面图表的人均购买饮料数量计算:这一天景区内若有50万游客,那么这一天购买的饮料的总数是多少?
表一:
出口 | B | C |
人均购买饮料数量(瓶) | 3 | 2 |
(3)若每瓶饮料要消耗0.5元处理包装的环保费用,该日需要花费多少钱处理这些饮料瓶?由此请你对游客做一点环保宣传建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在利用正六面体骰子进行频率估计概率的实验中,小闽同学统计了某一结果朝上的频率,绘出的统计图如图所示,则符合图中情况的可能是( )
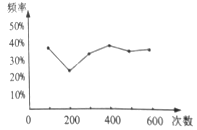
A. 朝上的点数是6的概率B. 朝上的点数是偶数的概率
C. 朝上的点数是小于4的概率D. 朝上的点数是3的倍数的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
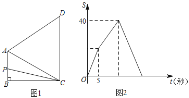
A. 10B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1).若以C,D,E(E在格点上)为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
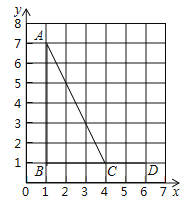
A. (6,0) B. (4,2) C. (6,5) D. (6,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连接AC,BC,作∠APC的平分线交AC于点D.
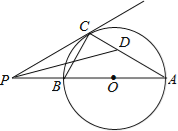
下列结论正确的是 (写出所有正确结论的序号)
①△CPD∽△DPA;
②若∠A=30°,则PC=![]() BC;
BC;
③若∠CPA=30°,则PB=OB;
④无论点P在AB延长线上的位置如何变化,∠CDP为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,过点A作AD⊥AB交⊙O于点D,交BC于点E,点F在DA的延长线上,且∠ABF=∠C .
(1)求证:BF是⊙O的切线;
(2)若AD=4,cos∠ABF=![]() ,求BC的长.
,求BC的长.
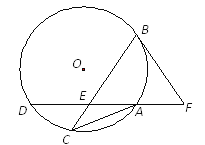
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com