
【题目】如图1,△ABC~△ADE,∠BAC=∠DAE=90°,AB=6,AC=8,点D在线段BC上运动,
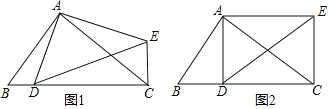
(1)如图1,求证:△ABD∽△ACE
(2)如图2,当AD⊥BC时,判断四边形ADCE的形状,并证明.
(3)当点D从点B运动到点C时,设P为线段DE的中点,在点D的运动过程中,求CP的最小值.
【答案】(1)见解析;(2)四边形ADCE是矩形,见解析;(3)4
【解析】
(1)先判断出∠BAD=∠CAE,再判断出![]() ,即可得出结论;
,即可得出结论;
(2)先判断出∠ADB=90°,根据相似判断出∠AEC=90°,即可得出结论;
(3)先判断出CP最小时,AD最小,再根据直角三角形的面积的计算方法求出AD的最小值,即可得出结论.
解:(1)∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
∵△ABC~△ADE,
∴![]() ,
,
∴△ABD∽△ACE;
(2)∵AD⊥BC,
∴∠ADC=∠ADB=90°,
由(1)知△ABD∽△ACE,
∴∠AEC=∠ADB=90°,
∵∠DAE=90°,
∴∠ADC=∠DAE=∠AEC=90°,
∴四边形ADCE是矩形;
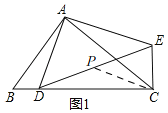
(3)如图1,
连接CP,
在Rt△ABC中,AB=6,AC=8,根据勾股定理得,BC=10,
∵△ABC∽△ADE,
∴![]() ,
,
∴DE=![]() =
=![]() AD=
AD=![]() AD,
AD,
由(1)知,△ABD∽△ACE,
∴∠ABD=∠ACE,
∵∠BAC=90°,
∴∠ABD+∠ACB=90°,
∴∠BCE=∠ACB+∠ACE=∠ACB+∠ABD=90°,
∴CP=![]() DE,
DE,
∵DE=![]() AD,
AD,
∴CP=![]() ×
×![]() AD=
AD=![]() AD,
AD,
要CP最小,则AD最小,
即:当AD⊥BC时,AD最小,
∵S△ABC=![]() ABAC=
ABAC=![]() BCAD最小,
BCAD最小,
∴AD最小=![]() ,
,
即:CP最小=![]() AD最小=
AD最小=![]() ×
×![]() =4,
=4,
即CP的最小值为4.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】一节数学课后,老师布置了一道课后练习题:
如图1,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .求证:
.求证:![]() .
.
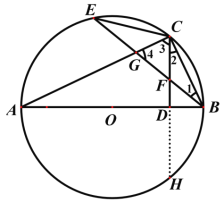

图1 图2
(1)本题证明的思路可用下列框图表示:
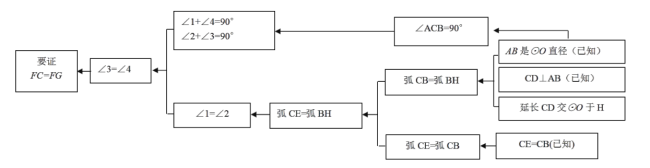
根据上述思路,请你完整地书写本题的证明过程.
(2)如图2,若点![]() 和点
和点![]() 在
在![]() 的两侧,
的两侧,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,其余条件不变,(1)中的结论还成立吗?请说明理由;
,其余条件不变,(1)中的结论还成立吗?请说明理由;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
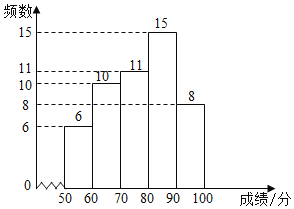
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 上的点,且
上的点,且![]() ,联结
,联结![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时,如果
时,如果![]() 是以
是以![]() 为腰的等腰三角形,求线段
为腰的等腰三角形,求线段![]() 的长;
的长;
(3)当![]() 时,求
时,求![]() 的正切值.(用含
的正切值.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
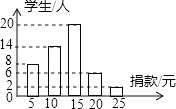
【题目】在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图,
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有800名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
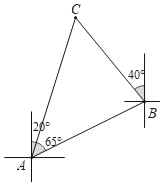
【题目】如图,一艘船由A港沿北偏东65°方向航行90![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种成本为每件![]() 元的商品,销售过程中发现,每月销售量
元的商品,销售过程中发现,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系可近似看作一次函数
(元)之间的关系可近似看作一次函数![]() .商场销售该商品每月获得利润为
.商场销售该商品每月获得利润为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果商场销售该商品每月想要获得![]() 元的利润,那么每件商品的销售单价应为多少元?
元的利润,那么每件商品的销售单价应为多少元?
(3)商场每月要获得最大的利润,该商品的销售单价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() ,甲、乙两人从两地出发相向而行,甲先出发.图中
,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离
表示两人离![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系,结合图象,下列结论错误的是( )
的关系,结合图象,下列结论错误的是( )
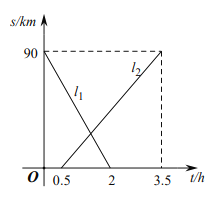
A.![]() 是表示甲离
是表示甲离![]() 地的距离与时间关系的图象
地的距离与时间关系的图象
B.乙的速度是![]()
C.两人相遇时间在![]()
D.当甲到达终点时乙距离终点还有![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的动点(不与
边上的动点(不与![]() 重合),点
重合),点![]() 在
在![]() 边上,并且满足
边上,并且满足![]() .
.
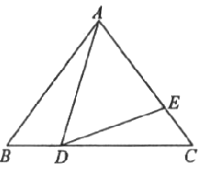
(1)求证:![]() ;
;
(2)若![]() 的长为
的长为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)当(2)中的![]() 最短时,求
最短时,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com