
����Ŀ���ۺϣ�
��1����ͼ�٣���������ABCD�У���AEF�Ķ���E��F�ֱ���BC��CD���ϣ���AG�������εı߳���ȣ����EAF�Ķ�����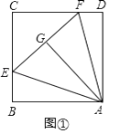
��2����ͼ�ڣ���Rt��ABD�У���BAD=90�㣬AB=AD����M��N��BD���ϵ��������㣬�ҡ�MAN=45�㣬����ABM�Ƶ�A��ʱ����ת90������ADHλ�ã�����NH�����ж�MN��ND��BM֮���������ϵ����˵�����ɣ�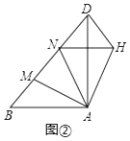
��3����ͼ���У�����BD�ֱ�AE��AF�ڵ�M��N����DN=3 ![]() ��BM=3
��BM=3 ![]() ����MN�ij���
����MN�ij���
���𰸡�
��1���⣺��ͼ�٣�
��Rt��ABE��Rt��AGE�� ![]() ��
��
���ABE�ա�AGE��HL����
���BAE=��GAE��
ͬ����GAF=��DAF��
���EAF= ![]() =45�㣻
=45�㣻
��2���⣺��ͼ�ڣ�
�ߡ�BAD=90�㣬AB=AD��
���ABD=��ADB=45�㣬
������֪��ABM��ADH��
���ADH=��ABM=45�㣬AH=AM��
���BDH=90�㣬
�ߡ�MAN=45�㣬
���BAM+��DAN=45�㣬
���DAN+��DAH=45�㣬
����NAH=45�㣬
�ڡ�AMN�͡�AHN�У�
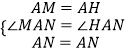 ��
��
���AMN�ա�AHN��SAS����
��HN=MN��
��Rt��NDH��NH2=DH2+ND2��
��MN2=BM2+DN2
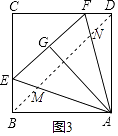
��3���⣺��ͼ�ۣ��ɣ�2���н��ۿ�֪��MN2=BM2+DN2��
��DN=3 ![]() ��BM=3
��BM=3 ![]() ��
��
��MN= ![]() =9��
=9��
����������1����HL֤����ABE�ա�AGE����AGF�ա�ADF���ɣ�ֻ��֤��һ��ȫ�ȣ���һ��ͬ����֤����2����֤����AMN�ա�AHN������֤����NHD��ֱ�������μ��ɣ���3�����ã�2���н��۽������̣���֮���ɣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������P����ABC�ڲ�����ϵĵ㣨������⣩������PAB����PBC����PCA�У���������һ������������ABC���ƣ���Ƶ�P����ABC�������Ƶ㣮
���磺��ͼ1����P����ABC���ڲ�����PBC=��A����PCB=��ABC������BCP�ס�ABC������PΪ��ABC�������Ƶ㣮
����������ѧ֪ʶ������������ϣ�����������⣺
��ƽ��ֱ������ϵ�У���M������C��![]()
![]() �ϵ�����һ�㣬��N��x���������ϵ�����һ�㣮
�ϵ�����һ�㣬��N��x���������ϵ�����һ�㣮
��1�� ��ͼ2����P��OM��һ�㣬��ONP=��M, ��˵����P����MON�������Ƶ㣻 ����M��������![]() ����N��������
����N��������![]() ʱ�����P �����ꣻ
ʱ�����P �����ꣻ
��2�� ��ͼ3������M��������![]() ����N��������
����N��������![]() ʱ������MON�������Ƶ�����ꣻ
ʱ������MON�������Ƶ�����ꣻ
��3�� �Ƿ���ڵ�M�͵�N,ʹ��MON�������Ƶ�,�������ڣ���ֱ��д������������ꣻ�������ڣ���˵�����ɣ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��PΪ����AB�ϵ�һ�㣬��BPΪ����������BPEF��ʹ��F���߶�CB���ӳ����ϣ�����EA��EC��

��1����ͼ1������P���߶�AB���ӳ����ϣ���֤��EA=EC��
��2����ͼ2������P���߶�AB���е㣬����AC���ж���ACE����״����˵�����ɣ�
��3����ͼ3������P���߶�AB�ϣ�����AC����EPƽ����AECʱ����AB=a��BP=b����a��b����AEC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չѧ���ĺ�������������ѧ�����ۺ�������ijѧУ�ƻ���������ѡ�Σ��������赸���滭���鷨��ѧУ��ȡ��������ķ��������ʾ����飨ÿ���������ѧ������ѡ�����ֻ��ѡ������һ�ţ����Ե������������������Ƴ�����������������ͳ��ͼ������ͼ��������Ϣ����������⣺

��1�����ε����ѧ������ �ˣ�������ͳ��ͼ�У�m��ֵ�� ��
��2��������ͳ��ͼ����������
��3���ڱ������ѧ���У�ѡ���鷨����2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ����ѧУ�μ�ij������֯���鷨�����д������ȡ��2��ͬѧǡ����1����ͬѧ��1��Ůͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һֱ�������������������ֱ���A��B���㣬P���߶�AB������һ�㣨�������˵㣩����P�ֱ�����������Ĵ�������������Χ�ɵľ��ε��ܳ�Ϊ20�����ֱ�ߵĺ�������ʽ�ǣ� �� 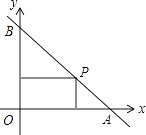
A.y=x+10
B.y=��x+10
C.y=x+20
D.y=��x+20
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com