
| 3 |
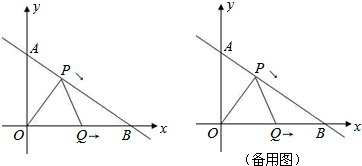
| OA |
| OB |
| 3 | ||
3
|
| ||
| 3 |
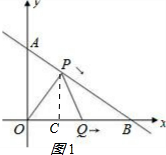
| 3 |
| OA2+OB2 |
32+(3
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
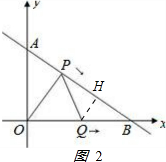 ,
,| PB |
| 2 |
| 6-t |
| 2 |
| 3 |
| HB |
| QB |
| ||
| 2 |
| ||
| 2 |
| 6-t |
| 2 |
| ||
| 2 |
| 3 |
6
| ||
| 11 |


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
 全市七运会在塖州市举办,在800m比赛中,甲乙两名运动员同时起跑,刚跑出160m后,甲不慎摔得,他又迅速的爬起来继续投入比赛,并取得了优异的成绩.如图分别表示甲乙两名运动员所跑路程y(m)与比赛时间x(s)之间的关系,根据图象可得:甲摔倒后是在距离起点
全市七运会在塖州市举办,在800m比赛中,甲乙两名运动员同时起跑,刚跑出160m后,甲不慎摔得,他又迅速的爬起来继续投入比赛,并取得了优异的成绩.如图分别表示甲乙两名运动员所跑路程y(m)与比赛时间x(s)之间的关系,根据图象可得:甲摔倒后是在距离起点查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线与x轴相交于点A,与y轴相交于点B.
如图,直线与x轴相交于点A,与y轴相交于点B.| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com