
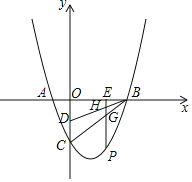
����Ŀ����֪������y��x2��2x��3��x�ύ�ڵ�A��B����y�ύ�ڵ�C����DΪOC�е㣬��P���������ϣ�
��1��ֱ��д��A��B��C��D���ꣻ
��2����P�ڵ������ޣ�����P��PE��x�ᣬ����ΪE��PE��BC��BD��G��H���Ƿ���������ĵ�P��ʹPG��GH��HE�������ڣ������P���ꣻ�������ڣ���˵�����ɣ�
��3����ֱ��y��![]() x+t��������y��x2��2x��3��x���·����������㣬ֱ��д��t��ȡֵ��Χ��
x+t��������y��x2��2x��3��x���·����������㣬ֱ��д��t��ȡֵ��Χ��
���𰸡���1��A(��1��0)��B(3��0)��C(0����3)��D(0����![]() )����2�����ڣ�(
)����2�����ڣ�(![]() ����
����![]() )����3����
)����3����![]() ��t����1
��t����1
��������
��1����ͨ�����κ����Ľ���ʽ�г����̣����������ص�����ꣻ
��2�����ڣ������ֱ��BC��ֱ��BD�Ľ���ʽ�����P������Ϊ��x��x2��2x��3������E��x��0����H��x��![]() x��
x��![]() ����G��x��x��3�����г���ʽ���̣����������P���ꣻ
����G��x��x��3�����г���ʽ���̣����������P���ꣻ
��3�����ֱ��y��![]() x+t������Bʱt��ֵ�����г���ֱ��y��
x+t������Bʱt��ֵ�����г���ֱ��y��![]() x+t��������y��x2��2x��3ֻ��һ������ʱ�ķ��̣�ʹ�����б�ʽΪ0�����t��ֵ������д��t��ȡֵ��Χ��
x+t��������y��x2��2x��3ֻ��һ������ʱ�ķ��̣�ʹ�����б�ʽΪ0�����t��ֵ������д��t��ȡֵ��Χ��
�⣺��1����y��x2��2x��3�У�
��x��0ʱ��y����3����y��0ʱ��x1����1��x2��3��
��A����1��0����B��3��0����C��0����3����
��DΪOC���е㣬
��D��0����![]() ����
����
��2�����ڣ��������£�
��ֱ��BC�Ľ���ʽΪy��kx��3��
����B��3��0������y��kx��3��
���k��1��
��ֱ��BC�Ľ���ʽΪy��x��3��
��ֱ��BD�Ľ���ʽΪy��mx��![]() ��
��
����B��3��0������y��mx��![]() ��
��
���m��![]() ��
��
��ֱ��BD�Ľ���ʽΪy��![]() x��
x��![]() ��
��
���P��������x��x2��2x��3������E��x��0����H��x��![]() x��
x��![]() ����G��x��x��3����
����G��x��x��3����
��EH����![]() x+
x+![]() ��HG��
��HG��![]() x��
x��![]() ����x��3������
����x��3������![]() x+
x+![]() ��GP��x��3����x2��2x��3������x2+3x��
��GP��x��3����x2��2x��3������x2+3x��
��EH��HG��GPʱ����![]() x+
x+![]() ����x2+3x��
����x2+3x��
���x1��![]() ��x2��3����ȥ����
��x2��3����ȥ����
���P��������![]() ����
����![]() ����
����
��3����ֱ��y��![]() x+t������Bʱ��
x+t������Bʱ��
����B��3��0������y��![]() x+t��
x+t��
�ã�t����1��
��ֱ��y��![]() x+t��������y��x2��2x��3ֻ��һ������ʱ������
x+t��������y��x2��2x��3ֻ��һ������ʱ������![]() x+t��x2��2x��3ֻ��һ���⣬
x+t��x2��2x��3ֻ��һ���⣬
��x2��![]() x��3��t��0��
x��3��t��0��
������![]() ��2��4����3��t����0��
��2��4����3��t����0��
���t����![]() ��
��
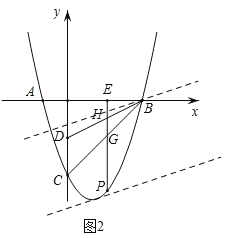
����ͼ2���Կ�������ֱ��y��![]() x+t��������y��x2��2x��3��x���·�����������ʱ��t��ȡֵ��ΧΪ����
x+t��������y��x2��2x��3��x���·�����������ʱ��t��ȡֵ��ΧΪ����![]() ��t����1ʱ��
��t����1ʱ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ֪��y=-2x+4��x�ᡢy��ֱ��ڵ�A��C����OA��OCΪ���ڵ�һ��������������OABC��

��1�����A��C�����ꣻ
��2������ABC���ۣ�ʹ�õ�A�����C�غϣ��ۺ۽�AB�ڵ�D����ֱ��CD�Ľ���ʽ��ͼ������
��3��������ƽ���ڣ��Ƿ���ڵ�P������B�⣩��ʹ����APC����ABCȫ�ȣ������ڣ���ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
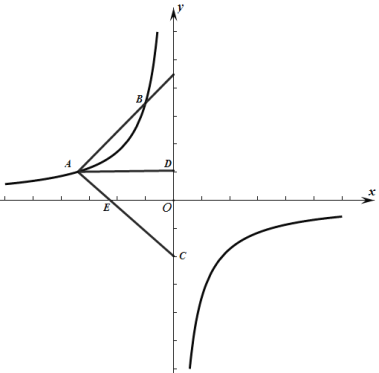
����Ŀ����ͼ������������![]() ��ͼ����
��ͼ����![]() ������
������![]() �뷴����������ͼ�����һ������Ϊ
�뷴����������ͼ�����һ������Ϊ![]() ,����
,����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ,��
,��![]() �ύ�ڵ�
�ύ�ڵ�![]() �ᣬ ����Ϊ
�ᣬ ����Ϊ![]() ��
��
![]() ���������Ľ���ʽ;
���������Ľ���ʽ;
![]() ��
��![]() �ij�
�ij�
![]() ��
��![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() ���ƣ������ڣ����������������
���ƣ������ڣ����������������![]() �����꣬�������ڣ���˵�����ɣ�
�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ���A=60����AB=2������BEF�İ뾶Ϊ2��Բ�Ľ�Ϊ60������ͼ����Ӱ���ֵ�����ǣ� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽס�����̨��װ����װ������Ϊ300g�Ĵ�װʳƷ�и���ȡ10���������ʵ���������£���λ��g��
�ף�301��300��305��302��303��302��300��300��298��299
�ң�305��302��300��300��300��300��298��299��301��305
��1���ֱ����ס���������������ƽ�����ͷ��
��2���Ƚ�����̨��װ����װ�������ȶ��ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ�����![]() ��
��![]() �����ͺŵĻ����˼ӹ��������֪
�����ͺŵĻ����˼ӹ��������֪![]() �ͻ����˱�
�ͻ����˱�![]() �ͻ�����ÿСʱ��ӹ�
�ͻ�����ÿСʱ��ӹ�![]() ���������
���������![]() �ͻ����˼ӹ�
�ͻ����˼ӹ�![]() ������õ�ʱ����
������õ�ʱ����![]() �ͻ����˼ӹ�
�ͻ����˼ӹ�![]() ��������õ�ʱ����ͬ��
��������õ�ʱ����ͬ��
(1)��![]() ,
,![]() �����ͺŵĻ�����ÿСʱ�ֱ�ӹ��������;
�����ͺŵĻ�����ÿСʱ�ֱ�ӹ��������;
(2)�ù����ƻ��ɹ�![]() ��
��![]() �����ͺŵĻ����˹�
�����ͺŵĻ����˹�![]() ̨��Ҫ��ÿСʱ�ӹ������������
̨��Ҫ��ÿСʱ�ӹ������������![]() ���������ٹ���
���������ٹ���![]() �ͻ����˶���̨?
�ͻ����˶���̨?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С������ö�ʵؾ��ȵ�Ӳ������Ϸ����Ϸ�����ǣ�ͬʱ��������öӲ�ң�������ö�������ϣ�һö�������£���С��Ӯ��������ö�������£�һö�������ϣ���С��Ӯ�������Ϸ�����˫����ƽ����������״ͼ���б���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC����ABC��90����AB��BC��2���ֽ�Rt��ABC�Ƶ�A��ʱ����ת30���õ���AED����ͼ����Ӱ���ֵ������__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����dzߣ���![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����ͼ�ڷţ���
����ͼ�ڷţ���![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ�뷽����ת
˳ʱ�뷽����ת![]() ��
��![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ֵΪ�� ��
��ֵΪ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com