
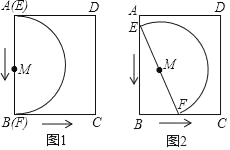
【题目】在矩形ABCD中,AB=8,BC=6,以EF为直径的半圆M如图所示位置摆放,点E与点A重合,点F与点B重合,点F从点B出发,沿射线BC以每秒1个单位长度的速度运动,点E随之沿AB下滑,并带动半圆M在平面滑动,设运动时间t(t≥0),当E运动到B点时停止运动.
发现:M到AD的最小距离为 ,M到AD的最大距离为 .
思考:①在运动过程中,当半圆M与矩形ABCD的边相切时,求t的值;
②求从t=0到t=4这一时间段M运动路线长;
探究:当M落在矩形ABCD的对角线BD上时,求S△EBF.
【答案】4、8;①当t=0或t=4或t=8时,半圆M与矩形ABCD的边相切;②![]() π;
π;![]()
【解析】
发现:当点A与点E重合时,点M与AD的距离最小,当点E与点B重合时,点M到AD的距离最大,据此可得;
思考:①根据题意知t=0时半圆M与AD、BC相切,当t=8时半圆M与AB相切,当半圆M与CD相切时,设切点为N,延长NM交AB于点Q,由M是EF的中点且QM∥BF知![]() ,据此可得t=BF=2QM=4;
,据此可得t=BF=2QM=4;
②t=0到t=4这一段时间点M运动的路线长为![]() ,由Rt△EBF中BM=MF=BF=4知△BMF是等边三角形,据此可得∠MBF=60°、∠MBM′=30°,利用弧长公式计算可得;
,由Rt△EBF中BM=MF=BF=4知△BMF是等边三角形,据此可得∠MBF=60°、∠MBM′=30°,利用弧长公式计算可得;
探究:当点M落在BD上时,由四边形BCDA是矩形知∠OAB=∠OBA,由BM是Rt△EBF斜边EF的中线知BM=EM、∠MBE=∠BEM,得出∠OAB=∠BEM及EF∥AC,从而知![]() ,据此解答可得.
,据此解答可得.
解:发现:当点A与点E、点B与点F重合时,点M与AD的距离最小,最小距离为4;
当点E与点B重合时,点M到AD的距离最大,最大距离为8;
故答案为:4、8;
思考:①由于四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,
∴当t=0时,半圆M既与AD相切、又与BC相切;
如图1,当半圆M与CD相切时,设切点为N,
∴∠MNC=90°,
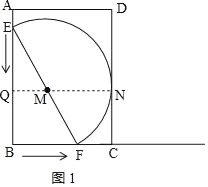
延长NM交AB于点Q,
∵∠B=∠C=90°,
∴四边形BCNQ是矩形,
∴QN=BC=6,QM=QN﹣MN=2,
∵M是EF的中点,且QM∥BF,
∴![]() ,
,
∴t=BF=2QM=4;
当t=8时,∵∠ABM=90°,
∴半圆M与AB相切;
综上,当t=0或t=4或t=8时,半圆M与矩形ABCD的边相切;
②如图2,t=0到t=4这一段时间点M运动的路线长为![]() ,
,
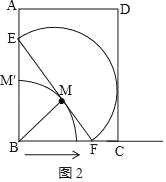
t=4时,BF=4,
由于在Rt△EBF中,EM=MF=4,
∴BM=MF=4,
∴BM=MF=BF=4,
∴△BMF是等边三角形,
∴∠MBF=60°,
∴∠MBM′=30°,
则![]() =
=![]() ;
;
探究:如图3,
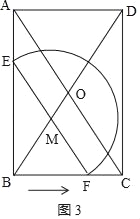
∵AB=8、AD=6,
∴BD=10,
当点M落在BD上时,
∵四边形BCDA是矩形,
∴OB=OA,
∴∠OAB=∠OBA,
∵BM是Rt△EBF斜边EF的中线,
∴BM=EM,
∴∠MBE=∠BEM,
∴∠OAB=∠BEM,
∴EF∥AC,
∴![]() ,
,
∵S△ABC=24,
∴S△EBF=![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,1),B(1,2),点P在x轴上运动,当点P到A、B两点距离之差的绝对值最大时,点P的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,![]() ,则a2+b2=c2
,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,![]() ,则a2+b2=c2
,则a2+b2=c2
查看答案和解析>>
科目:初中数学 来源: 题型:
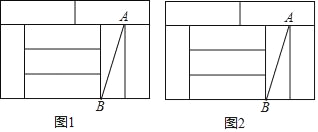
【题目】如图,8个完全相同的小矩形拼成了一个大矩形,AB是其中一个小矩形的对角线,请在大矩形中完成下列画图,要求:①仅用无刻度的直尺;②保留必要的画图痕迹.
(1)在图1中画出一个45°的角,使点A或者点B是这个角的顶点,且AB为这个角的一边.
(2)在图2中画出线段AB的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
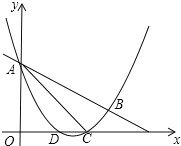
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
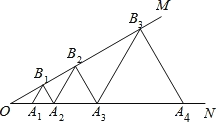
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
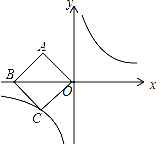
【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4![]() ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.
(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com