
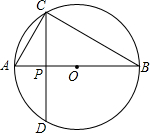
 如图所示,点C在以AB为直径的⊙O上,CD⊥AB于点P.求当AP=
如图所示,点C在以AB为直径的⊙O上,CD⊥AB于点P.求当AP=| 1 |
| 4 |
 |
| AC |
 |
| AD |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
 |
| AC |
 |
| AD |
| CP |
| PB |
| AP |
| CP |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| CP |
| PB |
| ||
| 3 |


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
| a-b |
| a+b |
| A、大于0 | B、小于0 |
| C、等于0 | D、不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
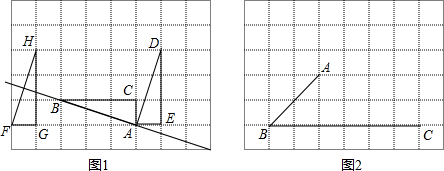
 在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.
在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com