
【题目】(1)问题提出:
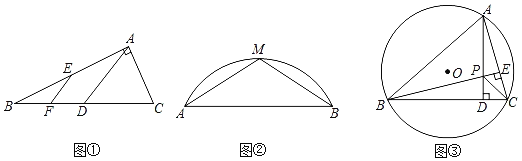
如图①,在Rt△BAC中,∠BAC=90°,点D,E分别是CB,AB的中点,点F是BD的中点,若AB=8,AC=6,则EF= ;
(2)问题探究:
如图②,已知:M是弓形AB上的中点,AB=24,弓形AB的高是8,则对应⊙O的面积为多少?(结果保留根号或π)
(3)问题解决:
如图③,在半径为5的⊙O中,弦BC=8,点A为优弧BC上的动点,过点A作AD⊥BC于点D,过点B作BE⊥AC于点E.AD和BE交于点P,连接PC,试求△PBC面积的最大值.
【答案】(1)![]() ;(2)169π;(3)证明见解析,点P的运动轨迹是弧线,8.
;(2)169π;(3)证明见解析,点P的运动轨迹是弧线,8.
【解析】
(1)如图①中,利用勾股定理求出BC,利用直角三角形斜边中线的性质求出AD,利用三角形的中位线定理即可解决问题.
(2)如图②中,设圆心为O,连接OM,OB,OM交AB于E.设OB=r.利用勾股定理构建方程即可解决问题.
(3)首先证明∠BPC是定值,推出点P的运动轨迹是弧线,如图3-2中,当A,O,D共线时,PD定值最大,此时△PBC的面积最大.
解:(1)如图①中,
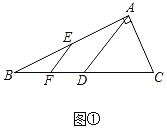
在Rt△ABC中,∵AB=8,AC=6,
∴BC=![]() =10,
=10,
∵BD=CD,
∴AD=![]() BC=5,
BC=5,
∵BE=EA,BF=FD,
∴EF=![]() AD=
AD=![]() ,
,
故答案为![]() .
.
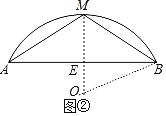
(2)如图②中,设圆心为O,连接OM,OB,OM交AB于E.设OB=r.
∵![]()
∴OM⊥BA,EM=8,
∴AE=EB=12
在Rt△OEB中,∵OE2+EB2=OB2
∴(r﹣8)2+122=r2,
∴r=13,
∴对应⊙O的面积为169π.
(3)如图3﹣1中,延长CP交AB于F.
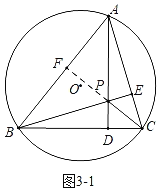
∵在半径为5的⊙O中,弦BC=8,
∴∠BAC是定值,设∠BAC=α,
∵AD,BE是高,
∴CF也是△ABC的高,
∴∠ABE=∠ACF=90°﹣α,
∵∠BPD=∠ABP+∠BAP,∠CPD=∠ACP+∠CAP,
∴∠BPC=∠ABP+∠BAP+∠CAP+∠PCA=90°+90°﹣α=180°﹣α,
∴∠BPC是定值,
∴点P的运动轨迹是弧线,
如图3﹣2中,当A,O,D共线时,PD定值最大,此时△PBC的面积最大.
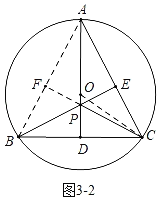
连接OC,在Rt△ODC中,OD=![]() =3,
=3,
∴AD=5+3=8,AC=AB=4![]() ,
,
∵![]() BCAD=
BCAD=![]() ABCF,
ABCF,
∴CF=![]() =
=![]() ,
,
∴AF=![]() =
=![]() ,
,
∵cos∠BAD=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PA=6,
∴PD=AD﹣PA=2,
∴△PBC的面积的最大值=![]() ×8×2=8.
×8×2=8.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
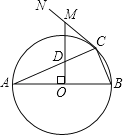
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
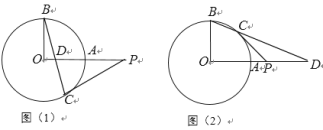
【题目】在⊙O中,半径OA丄OB,点D在OA或OA的延长线上(不与点O,A重合),直线BD交⊙O于点C,过C作⊙O的切线交直线OA于点P.
(1)如图(1),点D在线段OA上,若∠OBC=15°, 求∠OPC的大小;
(2)如图(2),点D在OA的延长线上,若∠OBC=65°,求∠OPC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个质地、大小都相同的小球分别标上数字2,-1,3后放入一个不透明的口袋搅匀,任意摸出一个小球,记下数字![]() 后,放回口袋中搅匀,再任意摸出一个小球,又记下数字b.这样就得到一个点的坐标
后,放回口袋中搅匀,再任意摸出一个小球,又记下数字b.这样就得到一个点的坐标![]() .
.
(1)求这个点![]() 恰好在函数
恰好在函数![]() 的图像上的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
的图像上的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)如果再往口袋中增加![]() 个标上数字2的小球,按照同样的操作过程,所得到的点
个标上数字2的小球,按照同样的操作过程,所得到的点![]() 恰好在函数
恰好在函数![]() 的图像上的概率是_________(请用含
的图像上的概率是_________(请用含![]() 的代数式直接写出结果).
的代数式直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家访是学校与家庭沟通的有效渠道,是形成教育合力的关键,是转化后进生的催化剂.某市教育局组织全市中小学教师开展家访活动活动过程中,教育局随机抽取了部分教师调查其近两周家访次数,将采集到的数据按家访次数分成五类,并分别绘制了下面的两幅不完整的统计图.
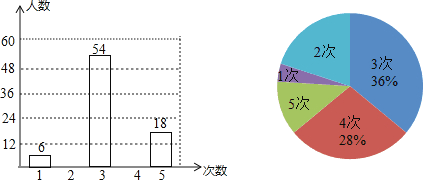
请根据以上信息,解答下列问题:
(1)请把条形统计图补充完整;
(2)所抽取的教师中,近两周家访次数的众数是 次,平均每位教师家访 次;
(3)若该市有12000名教师,请估计近两周家访不少于3次的教师有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 自变量
自变量![]() 的值和它对应的函数值
的值和它对应的函数值![]() 如下表所示:
如下表所示:
| … | 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | … |
(1)点M是该二次函数图象上一点,若点M纵坐标为8时,求点M的坐标;
(2)设该二次函数图象与![]() 轴的左交点为
轴的左交点为![]() ,它的顶点为
,它的顶点为![]() ,该图象上点
,该图象上点![]() 的横坐标为4,求
的横坐标为4,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
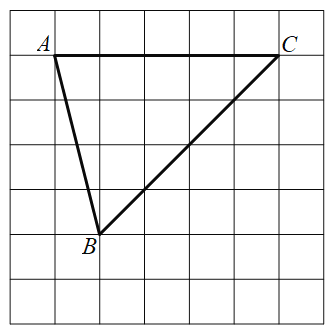
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.![]() 的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)作点A关于BC的对称点F;
(2)将线段AB向右平移得到线段DE,DE与BC交于点M,使![]() ;
;
(3)线段DE可以由线段BF绕点O顺时针旋转![]() 度而得到(B,F的对应点分别为D,E),在图中画出点O
度而得到(B,F的对应点分别为D,E),在图中画出点O
查看答案和解析>>
科目:初中数学 来源: 题型:
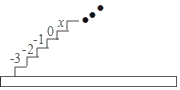
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣3,﹣2,﹣1,0,且任意相邻四个台阶上数的和都相等.
(1)求第五个台阶上的数x是多少?
(2)求前21个台阶上的数的和是多少?
(3)发现:数的排列有一定的规律,第n个﹣2出现在第 个台阶上;
(4)拓展:如果倩倩小同学一步只能上1个或者2个台阶,那么她上第一个台阶的方法有1种:1=1,上第二个台阶的方法有2种:1+1=2或2=2,上第三个台阶的方祛有3种:1+1+1=3、1+2=3或2+1=3,…,她上第五个台阶的方法可以有 种.
查看答案和解析>>
科目:初中数学 来源: 题型:
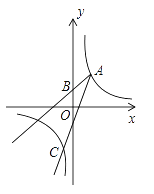
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com