
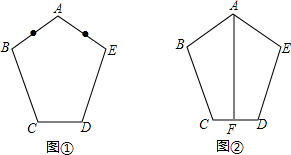
 如图①,已知五边形ABCDE,AB=AE,BC=ED,∠ABC=∠AED.
如图①,已知五边形ABCDE,AB=AE,BC=ED,∠ABC=∠AED.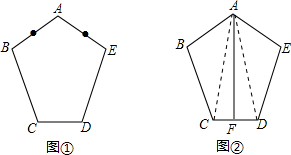 解:(1)该五边形有5条对角线;
解:(1)该五边形有5条对角线;
|
|


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
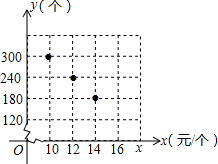 某商店准备购进一批茶杯进行销售,根据市场调查,这种茶杯一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
某商店准备购进一批茶杯进行销售,根据市场调查,这种茶杯一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
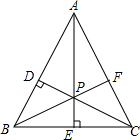 如图,△ABC边AB、BC的垂直平分线交于点P.
如图,△ABC边AB、BC的垂直平分线交于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com