
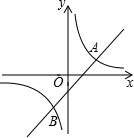
 ��ƽ��ֱ������ϵ�У�ֱ��y1=x+m��˫����y2=$\frac{k}{x}$���ڵ�A��B����֪��A��B�ĺ�����Ϊ2��-1��
��ƽ��ֱ������ϵ�У�ֱ��y1=x+m��˫����y2=$\frac{k}{x}$���ڵ�A��B����֪��A��B�ĺ�����Ϊ2��-1������ ��1�����ݴ���ϵ�������ɽ����
��2���ⷽ����$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$���ɽ��C��D���꣮
��3�����ۣ�x1+x2=x0����$\left\{\begin{array}{l}{y=ax+b}\\{y=\frac{k}{a}}\end{array}\right.$��ȥy�ã�ax2+bx-k=0������x1+x2=-$\frac{b}{a}$����ֱ��y=ax+b��x��Ľ���Ϊ��-$\frac{b}{a}$��0��������x0=-$\frac{b}{a}$������x1+x2=x0��
��� �⣺��1�������⣺$\left\{\begin{array}{l}{2+m=\frac{k}{2}}\\{-1+m=-k}\end{array}\right.$���$\left\{\begin{array}{l}{m=-1}\\{k=2}\end{array}\right.$��
��y1=x-1��y2=$\frac{2}{x}$��
��k=2��ֱ��y1=x-1��x��Ľ���Ϊ��1��0����
��2����$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$���$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.��\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$��
���Ե�C��1��2����D��-1��-2����
��3�����ۣ�x1+x2=x0��
���ɣ���$\left\{\begin{array}{l}{y=ax+b}\\{y=\frac{k}{a}}\end{array}\right.$��ȥy�ã�ax2+bx-k=0��
��ֱ��y=ax+b��˫����y=$\frac{k}{x}$��ak��0������������ĺ�����Ϊx1��x2��
��x1+x2=-$\frac{b}{a}$��
ֱ��y=ax+b��x��Ľ���Ϊ��-$\frac{b}{a}$��0����
��x0=-$\frac{b}{a}$��
��x1+x2=x0��
���� ���⿼�鷴����������һ�κ������й�֪ʶ������Ĺؼ������ⷽ������뽻������Ĺ�ϵ���������ν�ϵ�˼�룬�����п��������ͣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�����OABC������OC��OA�ֱ���x�ᡢy����������ϣ�����������y=$\frac{k}{x}$��x��0����AB�ཻ�ڵ�D����BC�ཻ�ڵ�E����BE=4EC���ҡ�ODE�������5����k��ֵΪ$\frac{25}{12}$��
��ͼ����ƽ��ֱ������ϵxOy�У�����OABC������OC��OA�ֱ���x�ᡢy����������ϣ�����������y=$\frac{k}{x}$��x��0����AB�ཻ�ڵ�D����BC�ཻ�ڵ�E����BE=4EC���ҡ�ODE�������5����k��ֵΪ$\frac{25}{12}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
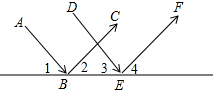 ��ͼ��ƽ�й���AB��DE����ͬһƽ�澵���䣬��ʱ��1=��2����3=��4����ô�������BC��EFƽ����˵�����ɣ�
��ͼ��ƽ�й���AB��DE����ͬһƽ�澵���䣬��ʱ��1=��2����3=��4����ô�������BC��EFƽ����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com