
【题目】如图,一条直线与反比例函数![]() 的图象交于A(1,4),B(4,n)两点,与x轴交于点D,AC⊥x轴,垂足为C.
的图象交于A(1,4),B(4,n)两点,与x轴交于点D,AC⊥x轴,垂足为C.

(1)求反比例函数的解析式及D点的坐标;
(2)点P是线段AD的中点,点E,F分别从C,D两点同时出发,以每秒1个单位的速度沿CA,DC运动,到点A,C时停止运动,设运动的时间为t(s).
①求证:PE=PF.②若△PEF的面积为S,求S的最小值.
【答案】(1)![]() ,D(5,0);(2)①证明见试题解析;②2.
,D(5,0);(2)①证明见试题解析;②2.
【解析】
(1)把点A的坐标代入![]() 求出k的值,即可得出反比例函数的解析式;求出点B的坐标,再求出直线AB的解析式,即可求出D点的坐标;
求出k的值,即可得出反比例函数的解析式;求出点B的坐标,再求出直线AB的解析式,即可求出D点的坐标;
(2)①由△ACD为等腰直角三角形,得出∠ADC=45°,得出CP=PD,CP⊥AD,∠ADC=∠ACP,即可得出△ECP≌△FDP,从而有PE=PF;
②由△ECP≌△FDP,得出∠EPC=∠FPD,得出∠EPF=∠CPD=90°,得到△EPF为等腰直角三角形,从而有△PEF的面积S=![]()
![]() ,当PE⊥AC时,PE最小,求出PE的最小值,即可得出S的最小值.
,当PE⊥AC时,PE最小,求出PE的最小值,即可得出S的最小值.
(1)把点A(1,4)代入![]() 得:k=4,∴反比例函数的解析式为:
得:k=4,∴反比例函数的解析式为:![]() ;把点B(4,n)代入得:n=1,∴B(4,1),设直线AB的解析式为y=kx+b,把A(1,4),B(4,1)代入y=kx+b得:
;把点B(4,n)代入得:n=1,∴B(4,1),设直线AB的解析式为y=kx+b,把A(1,4),B(4,1)代入y=kx+b得:![]() ,解得:k=﹣1,b=5,∴直线AB的解析式为:y=﹣x+5,当y=0时,x=5,∴D点坐标为:(5,0);
,解得:k=﹣1,b=5,∴直线AB的解析式为:y=﹣x+5,当y=0时,x=5,∴D点坐标为:(5,0);
(2)①∵A(1,4),C(1,0 ),D(5,0),AC⊥x轴于C,∴AC=CD=4,∴△ACD为等腰直角三角形,∴∠ADC=45°,∵P为AD中点,∴∠ACP=∠DCP=45°,CP=PD,CP⊥AD,∴∠ADC=∠ACP,∵点E,F分别从C,D两点同时出发,以每秒1个单位的速度沿CA,DC运动,∴EC=DF,在△ECP和△FDP中,∵CP=PD,∠ECP=∠PDF,EC=DF,∴△ECP≌△FDP(SAS),∴PE=PF;
②∵△ECP≌△FDP,∴∠EPC=∠FPD,∴∠EPF=∠CPD=90°,∴△PEF为等腰直角三角形,∴△PEF的面积S=![]()
![]() ,∴△PEF的面积最小时,EP最小,∵当PE⊥AC时,PE最小,此时EP最小值=
,∴△PEF的面积最小时,EP最小,∵当PE⊥AC时,PE最小,此时EP最小值=![]() CD=2,∴△PEF的面积S的最小值=
CD=2,∴△PEF的面积S的最小值=![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】某纪念品专卖店上周批发买进100件A纪念品和300件B纪念品,花费9600元;本周批发买进200件A纪念品和100件B纪念品,花费6200元.
(1)求每件A纪念品和B纪念品的批发价各为多少元?
(2)经市场调研,当A纪念品每件的销售价为30元时,每周可销售200件;当每件的销售价每增加1元,每周的销售数量将减少10件.当每件的销售价a为多少时,该纪态品专卖店销售A纪念品每周获得的利润W最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为400人,如表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
图书种类 | 频数 | 频率 |
科普常识 | 1600本 | B |
名人传记 | 1280本 | 0.32 |
漫画丛书 | A本 | 0.24 |
其它 | 160本 | 0.04 |
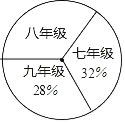
(1)求该校八年级的人数占全校总人数的百分率为 ;
(2)表中A= ,B= ;
(3)该校学生平均每人读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中有1个红球、1个白球,乙口袋中有1个红球、2个白球,这些球除颜色外无其他差别.
(1)从甲口袋中随机摸出1个球,恰好摸到红球的概率为 ;
(2)分别从甲、乙两个口袋中各随机摸出1个球,请用列表或画树状图的方法求摸出的2个球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形的顶点A(1,1),B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,C点的对应点记为C1.如果这样连续经过2019次变换后,则C2019的坐标为( )
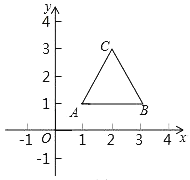
A. (﹣2017,﹣1﹣![]() )B. (﹣2017,1+
)B. (﹣2017,1+![]() )
)
C. (﹣2018,﹣1﹣![]() )D. (﹣2018,1+
)D. (﹣2018,1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+2
x2+2![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,对称轴与x轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交x轴交于点G.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,对称轴与x轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交x轴交于点G.
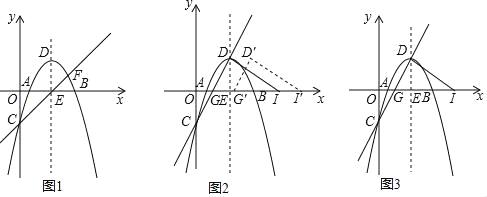
(1)如图1,求直线CE的解析式和顶点D的坐标;
(2)如图1,点P为直线CF上方抛物线上一点,连接PC、PF,当△PCF的面积最大时,点M是过P垂直于x轴的直线l上一点,点N是抛物线对称轴上一点,求FM+MN+NO的最小值;
(3)如图2,过点D作DI⊥DG交x轴于点I,将△GDI沿射线GB方向平移至△G′D′I′处,将△G′D′I′绕点D′逆时针旋转α(0<α<180°),当旋转到一定度数时,点G′会与点I重合,记旋转过程中的△G′D′I′为△G″D′I″,若在整个旋转过程中,直线G″I″分别交x轴和直线GD′于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:

①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com