
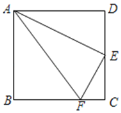
【题目】如图,在正方形ABCD中,点E是CD的中点,点F是BC上的一点,且BF=3CF,连接AE、AF、EF,下列结论:①∠DAE=30°,②△ADE∽△ECF,③AE⊥EF,④AE2=ADAF,其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据题意可得tan∠DAE的值,进而可判断①;设正方形的边长为4a,根据题意用a表示出FC,BF,CE,DE,然后根据相似三角形的判定方法即可对②进行判断;在②的基础上利用相似三角形的性质即得∠DAE=∠FEC,进一步利用正方形的性质即可得到∠DEA+∠FEC=90°,进而可判断③;利用相似三角形的性质即可判断④.
解:∵四边形ABCD是正方形,E为CD中点,∴CE=ED=![]() DC=
DC=![]() AD,
AD,
∴tan∠DAE=![]() ,∴∠DAE≠30°,故①错误;
,∴∠DAE≠30°,故①错误;
设正方形的边长为4a,则FC=a,BF=3a,CE=DE=2a,
∴![]() ,∴
,∴![]() ,又∠D=∠C=90°,
,又∠D=∠C=90°,
∴△ADE∽△ECF,故②正确;
∵△ADE∽△ECF,∴∠DAE=∠FEC,
∵∠DAE+∠DEA=90°∴∠DEA+∠FEC=90°,
∴AE⊥EF.故③正确;
∵△ADE∽△ECF,∴![]() ,∴AE2=ADAF,故④正确.
,∴AE2=ADAF,故④正确.
综上,正确的个数有3个,故选:C.


科目:初中数学 来源: 题型:
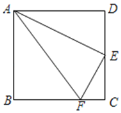
【题目】如图,是一座横跨沙颖河的斜拉桥,拉索两端分别固定在主梁l和索塔h上,索塔h垂直于主梁l,垂足为D.拉索AE,BF,CG的仰角分别是α,45°,β,且α+β=90°(α<β),AB=15m,BC=5m,CD=4m,EF=3FG,求拉索AE的长.(精确到1m,参考数据:![]() ≈2.24,
≈2.24,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
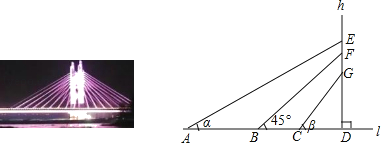
【题目】如图,已知在平面直角坐标系内有A(﹣1,2)、B(﹣3,1)、C(0,﹣1).
(1)画出△ABC关于O点成中心对称的△A1B1C1,直接写出B1:( , )
(2)将△ABC绕O点顺时针方向旋转90°后得到△A2B2C2,画出旋转后的图形并直接写出B2坐标:( , )
(3)求(2)中线段AB所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 逆时针旋转至点
逆时针旋转至点![]() 与点
与点![]() 重合,此时点
重合,此时点![]() 旋转至
旋转至![]() 处,则点
处,则点![]() 在旋转过程中形成的
在旋转过程中形成的![]() 、线段
、线段![]() 、点
、点![]() 在旋转过程中形成的
在旋转过程中形成的![]() 与线段
与线段![]() 所围成的阴影部分的面积为( )
所围成的阴影部分的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 是半圆弧的中点,点
是半圆弧的中点,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
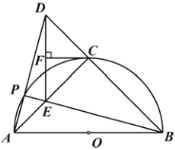
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为1,当点
的半径为1,当点![]() 运动到
运动到![]() 的三等分点时,求
的三等分点时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=![]() 的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
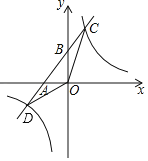
(1)求一次函数y=k1x+b与反比例函数y=![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出当x取什么值时,k1x+b<![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
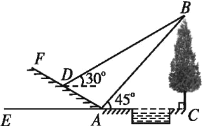
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com