Question

10．（1）如图1，在四边形ABCD中，AB=BC，∠ABC=80°，∠A+∠C=180°，点M是AD边上一点，把射线BM绕点B顺时针旋转40°，与CD边交于点N，请你补全图形，求MN，AM，CN的数量关系；
（2）如图2，在菱形ABCD中，点M是AD边上任意一点，把射线BM绕点B顺时针旋$\frac{1}{2}∠ABC$，与CD边交于点N，连结MN，请你补全图形并画出辅助线，直接写出AM，CN，MN的数量关系是MN＜AM+CN；
（3）如图3，正方形ABCD的边长是1，点M，N分别在AD，CD上，若△DMN的周长为2，则△MBN的面积最小值为$\sqrt{2}$-1．

Answer 1

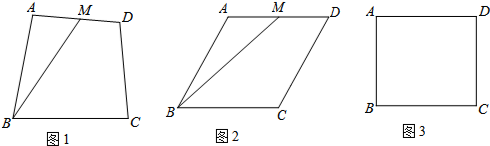
分析 （1）延长DA到点E，使AE=CN，连接BE，证明△ABE≌△CBN，得到∠EBA=∠CBN，BE=BN，AE=CN，所以∠EBN=∠ABC，因为∠ABC=80°，∠MBN=40°，所以∠EBM=∠NBM=40°，证明△EBM≌△NBM，得到EM=NM，因为EM=AM+AE，所以MN=AM+CN．
（2）以B为圆心，以BN的长为半径画弧，以A为圆心，以CN的长为半径画弧，两弧交于一点E，连接BE，AE，EM，所以BE=BN，AE=CN，根据四边形ABCD为菱形，得到BA=BC，所以△BAE≌△BCN（SSS），所以∠EBA=∠NBC，根据∠MBN=$\frac{1}{2}$∠ABC，∠ABC=∠ABM+∠MBN+∠NBC，得到$∠ABM+∠NBC=\frac{1}{2}∠ABC$，所以$∠ABM+∠EBA=\frac{1}{2}∠ABC$，得到∠EBM=∠MBN，证明△EBM≌△MBN，得到EM=MN，在△AEM中，EM＜AE+AM，所以MN＜AM+CN．
（3）延长DC至L，使CL=AM，则Rt△BCL≌Rt△BAM，故BL=BM，进而求证△BMN≌△BNL，即可求得∠MBN=∠NBL=45°设DN=x，DN=y，MN=z，根据x²+y²=z²，和x+y+z=2，整理根据△=4（z-2）²-32（1-z）≥0可以解题．

解答 解：（1）延长DA到点E，使AE=CN，连接BE，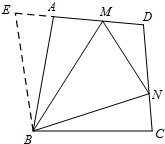

∵∠BAD+∠C=180°，
∴∠EAB=∠C，
在△ABE和△CBN中，
$\left\{\begin{array}{l}{AB=BC}\\{∠EAB=∠C}\\{AE=CN}\end{array}\right.$，
∴△ABE≌△CBN（SAS），
∴∠EBA=∠CBN，BE=BN，AE=CN，
∴∠EBN=∠ABC，
∵∠ABC=80°，∠MBN=40°，
∴∠EBM=∠NBM=40°，
在△EBM和△NBM中，
$\left\{\begin{array}{l}{BE=BN}\\{∠EBM=∠NBM}\\{BM=BM}\end{array}\right.$，
∴△EBM≌△NBM（SAS），
∴EM=NM，
∵EM=AM+AE，
∴MN=AM+CN．
（2）以B为圆心，以BN的长为半径画弧，以A为圆心，以CN的长为半径画弧，两弧交于一点E，连接BE，AE，EM，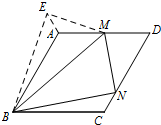

∴BE=BN，AE=CN，
∵四边形ABCD为菱形，
∴BA=BC，
∴△BAE≌△BCN（SSS），
∴∠EBA=∠NBC，
∵∠MBN=$\frac{1}{2}$∠ABC，∠ABC=∠ABM+∠MBN+∠NBC，
∴$∠ABM+∠NBC=\frac{1}{2}∠ABC$，
∴$∠ABM+∠EBA=\frac{1}{2}∠ABC$，
∴∠ABM+∠EBA=∠MBN，
即∠EBM=∠MBN，
在△EBM和△MBN中，
$\left\{\begin{array}{l}{BE=BN}\\{∠EBM=∠MBN}\\{BM=BM}\end{array}\right.$，
∴△EBM≌△MBN（SAS），
∴EM=MN，
在△AEM中，EM＜AE+AM，
∴MN＜AM+CN．
故答案为：MN＜AM+CN．
（3）如图：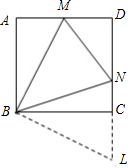

延长DC至L，使CL=AM，
∵∠A=∠BCL=90°，AB=BC，
∴Rt△BCL≌Rt△BAM（SAS），
∴BL=BM，
∵DM+DN+MN=2，AM+DM+DN+CN=1+1=2，
∴MN=AM+CN=CL+CN=NL，
∴△BMN≌△BNL（SSS），
设DN=x，DM=y，MN=z
x²+y²=z²，
∵x+y+z=2，
则x=2-y-z
∴（2-y-z）²+y²=z²，
整理得2y²+（2z-4）y+（4-4z）=0，
∴△=4（z-2）²-32（1-z）≥0，
即（z+2-2$\sqrt{2}$）（z+2+2$\sqrt{2}$）≥0，
又∵z＞0，
∴z≥2$\sqrt{2}$-2，
此时S_△BMN=S_△BML=$\frac{1}{2}$NL•AB=$\frac{1}{2}$MN=$\frac{1}{2}$z，
因此，当z=2$\sqrt{2}$-2，S_△BMN取到最小值为$\frac{1}{2}（2\sqrt{2}-2）$=$\sqrt{2}$-1．
故答案为：$\sqrt{2}$-1．

点评 本题考查了四边形，菱形和正方形，勾股定理在直角三角形中的应用，作辅助线，构建三角形全等是解题的关键．