
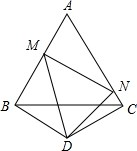
 如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由.
如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由. 解:△AMN的周长不变,面积发生变化,
解:△AMN的周长不变,面积发生变化,
|
|


科目:初中数学 来源: 题型:
 将图中的三张扑克牌背面朝上放在桌面上,从中随机摸出两张,并用这两张扑克牌上的数字组成一个两位数.请用画树状图(或列表)的方法,求组成的两位数是偶数的概率.
将图中的三张扑克牌背面朝上放在桌面上,从中随机摸出两张,并用这两张扑克牌上的数字组成一个两位数.请用画树状图(或列表)的方法,求组成的两位数是偶数的概率.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 项目 | A型 | B型 | C型 |
| 销售价(元) | 120 | 100 | 70 |
| 可供使用人数(人) | 80 | 50 | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com