
| 项目 | A型 | B型 | C型 |
| 销售价(元) | 120 | 100 | 70 |
| 可供使用人数(人) | 80 | 50 | 40 |
|
| 40 |
| 3 |
|


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
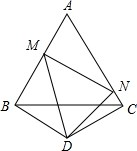 如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由.
如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com