
 如图,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.
如图,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.分析 (1)△PQR的边QR经过点B时,△ABQ构成等腰直角三角形,则有AB=AQ,由此列方程求出t的值;
(2)在图形运动的过程中,有三种情形,当1<t≤2时,当1<t≤2时,当2<t≤4时,进行分类讨论求出答案.
解答 解:(1)△PQR的边QR经过点B时,△ABQ构成等腰直角三角形,
∴AB=AQ,即3=4-t,
∴t=1.
即当t=1秒时,△PQR的边QR经过点B.
故答案为:1;
(2)①当0≤t≤1时,如答图1-1所示.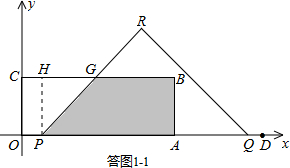
设PR交BC于点G,
过点P作PH⊥BC于点H,则CH=OP=2t,GH=PH=3.
S=S矩形OABC-S梯形OPGC
=8×3-$\frac{1}{2}$(2t+2t+3)×3
=$\frac{39}{2}$-6t;
②当1<t≤2时,如答图1-2所示.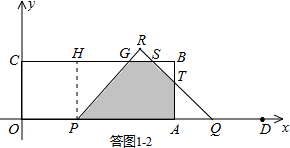
设PR交BC于点G,RQ交BC、AB于点S、T.
过点P作PH⊥BC于点H,则CH=OP=2t,GH=PH=3.
QD=t,则AQ=AT=4-t,
∴BT=BS=AB-AQ=3-(4-t)=t-1.
S=S矩形OABC-S梯形OPGC-S△BST
=8×3-$\frac{1}{2}$(2t+2t+3)×3-$\frac{1}{2}$(t-1)2
=-$\frac{1}{2}$t2-5t+19;
③当2<t≤4时,如答图1-3所示.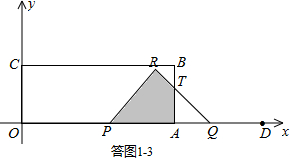
设RQ与AB交于点T,则AT=AQ=4-t.
PQ=12-3t,∴PR=RQ=$\frac{\sqrt{2}}{2}$(12-3t).
S=S△PQR-S△AQT
=$\frac{1}{2}$PR2-$\frac{1}{2}$AQ2
=$\frac{1}{4}$(12-3t)2-$\frac{1}{2}$(4-t)2
=$\frac{7}{4}$t2-14t+28.
综上所述,S关于t的函数关系式为:
S=$\left\{\begin{array}{l}{\frac{39}{2}-6t(0≤t≤1)}\\{-\frac{1}{2}{t}^{2}-5t+19(1<t≤2)}\\{{\frac{7}{4}t}^{2}-14t+28(2<t≤4)}\end{array}\right.$.
点评 本题主要考查了四边形综合,涉及动点与动线,复杂度较高,难度较大,第(2)问中,注意分类讨论周全,不要遗漏.


科目:初中数学 来源: 题型:解答题
 已知如图,在梯形ABCD中AB∥CD,对角线AC、BD交于点O,△ABC为边长为6的等边三角形,DC=2.
已知如图,在梯形ABCD中AB∥CD,对角线AC、BD交于点O,△ABC为边长为6的等边三角形,DC=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两枚骰子的点数的和可能为11 | B. | 两枚骰子的点数不可能相同 | ||
| C. | 两枚骰子的点数一定相同 | D. | 两枚骰子的点数的差可能为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com