
【题目】如图1,在△ABC中,AB=AC=20,tanB=![]() ,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
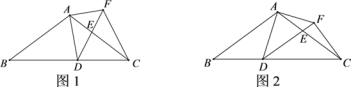
【答案】(1)详见解析;(2)![]() ;(3)点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.
;(3)点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.
【解析】
(1)根据两角对应相等的两个三角形相似证明即可;
(2)解直角三角形求出BC,由△ABD∽△DCE,推出![]() =
=![]() ,可得DB=
,可得DB=![]() =
=![]() =
=![]() ,由DE∥AB,推出
,由DE∥AB,推出![]() =
=![]() ,求出AE即可;
,求出AE即可;
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.过点F作FH⊥BC于点H,过点A作AM⊥BC于点M,AN⊥FH于点N,则∠NHA=∠AMH=∠ANH=90°,由△AFN∽△ADM,可得![]() =
=![]() =tan∠ADF=tanB=
=tan∠ADF=tanB=![]() ,推出CH=CM-MH=CM-AN=16-9=7,再利用等腰三角形的性质,求出CD即可解决问题.
,推出CH=CM-MH=CM-AN=16-9=7,再利用等腰三角形的性质,求出CD即可解决问题.
解:(1)∵AB=AC,
∴∠B=∠ACB.
∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠CDE.
∴△ABD∽△DCE.
(2)过点A作AM⊥BC于点M.
在Rt△ABM中,设BM=4k,则AM=BM·tanB=4k·![]() =3k.
=3k.
由勾股定理,得:AB2=AM2+BM2,得:
202=(3k)2+(4k)2,解得:k=4.
∵AB=AC,AM⊥BC,
∴BC=2BM=8k=32.
∵DE∥AB,
∴∠BAD=∠ADE.
又∵∠ADE=∠B,∠B=∠ACB,
∴∠BAD=∠ACB.
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴![]() =
=![]() ,则DB=
,则DB=![]() =
=![]() =
=![]() .
.
∵DE∥AB,
∴![]() =
=![]() ,
,
∴AE=![]() =
=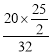 =
=![]() .
.
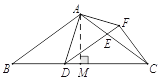
(3)点D在BC边上运动的过程中,存在某个位置,使得DF=CF.
过点F作FH⊥BC于点H,过点A作AM⊥BC于点M,AN⊥FH于点N,则∠NHA=∠AMH=∠ANH=90°.
∴四边形AMHN为矩形.
∴∠MAN=90°,MH=AN.
∵AB=AC,AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ×32=16.
×32=16.
在Rt△ABM中,由勾股定理,得:AM=![]() =
=![]() =12.
=12.
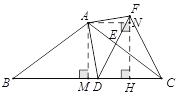
∵AN⊥FH,AM⊥BC,
∴∠ANF=90°=∠AMD.
∵∠DAF=90°=∠MAN,
∴∠NAF=∠MAD,
∴△AFN∽△ADM.
∴![]() =
=![]() =tan∠ADF=tanB=
=tan∠ADF=tanB=![]() .
.
∴AN=![]() AM=
AM=![]() ×12=9.
×12=9.
∴CH=CM-MH=CM-AN=16-9=
当DF=CF时,由点D不与点C重合时,可知△DFC为等腰三角形.
又∵FH⊥DC,
∴CD=2CH=14.
∴BD=BC-CD=32-14=18.
∴点D在BC边上运动 的过程中,存在某个位置,使得DF=CF,此时BD=18.


科目:初中数学 来源: 题型:
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
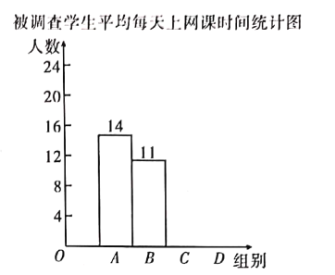
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平.为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
移动支付方式 | 支付宝 | 微信 | 其他 |
人数/人 |
| 200 | 75 |
请你根据上述统计表和统计图提供的信息.完成下列问题:
(1)在此次调查中,使用支付宝支付的人数;
(2)求表示微信支付的扇形所对的圆心角度数;
(3)某天该步行街人流量为10万人,其中30%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() .
.
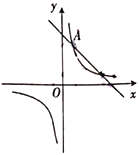
(1)求反比例函数和直线的解析式.
(2)将一次函数![]() 的图象沿
的图象沿![]() 轴向下平移
轴向下平移![]() 个单位长度,使平移后的图象与反比例函数
个单位长度,使平移后的图象与反比例函数![]() 的图象有且只有一个交点,求
的图象有且只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,与y轴交于点C,点D为顶点.
两点,与y轴交于点C,点D为顶点.
![]() 求抛物线解析式及点D的坐标;
求抛物线解析式及点D的坐标;
![]() 若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有
若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有![]() 且只有三个时,求直线l的解析式;
且只有三个时,求直线l的解析式;
![]() 如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到
如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到![]() ,旋转角为
,旋转角为![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 与抛物线的交点坐标.
与抛物线的交点坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,连结
,连结![]() ,且
,且![]() 平分
平分![]() .
.
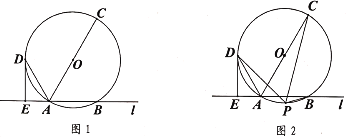
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)如图2,在(2)的条件下,点![]() 为
为![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,
,![]() ,问:线段
,问:线段![]() ,
,![]() ,
,![]() 之间存在什么数量关系?请说明理由.
之间存在什么数量关系?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com