
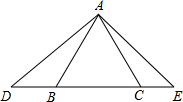
 如图.已知△ABC是等边三角形,D,B,C,E在同一条直线上,且∠DAE=120°.
如图.已知△ABC是等边三角形,D,B,C,E在同一条直线上,且∠DAE=120°.分析 (1)根据相似三角形的判定及已知可得到题中存在的相似三角形;
(2)根据相似三角形的对应边成比例及已知,即可求得DB、BC、CE之间的关系.
解答 解:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°.
∴∠D+∠DAB=60°,∠E+∠CAE=60°.
∵∠DAE=120°,
∴∠DAB+∠EAC=60°.
∴∠D=∠CAE,∠E=∠DAB.
∵∠D=∠D,∠E=∠E,
∴△DAE∽△DBA∽△ACE.
∴相似三角形共有3对.
(2)∵△DBA∽△ACE,
∴DB:AC=AB:CE.
∵AB=AC=BC,
∴BC2=DB•CE.
点评 此题考查了相似三角形的判定和性质:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
 已知:如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,且AB=18,AC=12.
已知:如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,且AB=18,AC=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
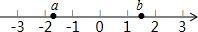 实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+2)^{2}}$+$\sqrt{(b-2)^{2}}$+$\sqrt{(a-b)^{2}}$.
实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+2)^{2}}$+$\sqrt{(b-2)^{2}}$+$\sqrt{(a-b)^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com