
【题目】关于x的方程|m-1|x2+2x-3=0.
(1)求证:当m≠1时,原方程总有两个不相等的实数根;
(2)若原方程的一个根是1,求此时m的值及方程的另一个根.
【答案】(1)见解析;(2)m=2或0,方程的另一个根为x2=-3.
【解析】
(1) 只要证明当m≠1时,判别式总大于0即可;
(2) 将x=2代入方程求出m,再解方程可求另一个根.
解:(1)∵m≠1
∴|m-1|![]() ;方程|m-1|x2+2x-3=0是一元二次方程
;方程|m-1|x2+2x-3=0是一元二次方程
由题可知:a=|m-1|,b=2,c=-3,
△=b2-4ac=42-4|m-1|![]() (-3)=16+12|m-1|>0,
(-3)=16+12|m-1|>0,
∴当m≠1时,原方程总有两个不相等的实数根;
(2)将x=1代入方程,有|m-1|+2-3=0,解得:m=2或0,
此时原方程为:x2+2x-3=0,
∴(x-1)(x+3)=0
∴x1=1,x2=-3,
因此方程的另一个根为x2=-3.


科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BC·AB=AC2,那么称线段AB被点C黄金分割。
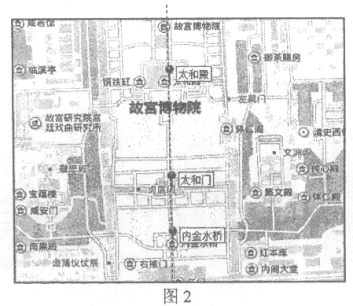
为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域。如图2,在我国古代紫禁城的中轴线上,太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割,已知太和殿到内金水桥的距离约为100丈,求太和门到太和殿之间的距离(![]() 的近似值取2.2)。
的近似值取2.2)。
查看答案和解析>>
科目:初中数学 来源: 题型:
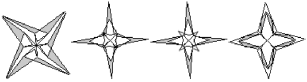
【题目】下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
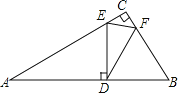
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
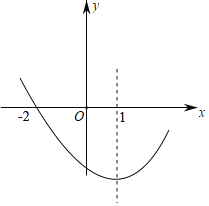
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直线x=1.有以下结论:
①abc>0;
②8a+c>0;
③若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;
④点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得PM⊥PN,则a的取值范围为a≥1;
⑤若方程a(x+2)(4﹣x)=﹣2的两根为x1,x2,且x1<x2,则﹣2≤x1<x2<4.
其中结论正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC 的一边长为 10,另两边长分别是方程 x2 14 x 48 0 的两个根若用一圆形纸片将此三角形完全覆盖,则该圆形纸片的最小半径是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表:
的几组对应值列表:

其中,![]() ________.
________.
(2)根据表格数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
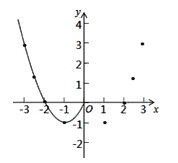
(3)观察函数图象,写出两条函数的性质:
________;
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com