
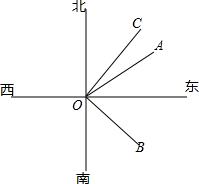
 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°.分析 (1)①根据和为90°的两个角互余,可得射线OC的方向;
②根据和为90°的两个角互余,可得答案,根据两个角的和为180°,这两个角互补,可得答案;
(2)根据OA是∠BON的角平线,可得∠NOA与∠NOB的关系,进而利用绝对值的性质求出m,n的值,可得答案.
解答 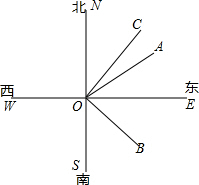 解:(1)①若m=50,m°+n°=90°,n=40,
解:(1)①若m=50,m°+n°=90°,n=40,
则射线OC的方向是北偏东40°;
②由∠BOS+∠BOE=90°,图中与∠BOE互余的角有∠BOS,
由m°的角与n°的角互余,∠BOE+COE=90°,
得图中与∠BOE互余的角有∠COE,
∠BOE+BOW=180°,∠BOE互补的角有∠BOW,∠SOC.
故答案为:北偏东40°;∠BOS、∠COE;∠BOW,∠SOC;
(2)∵射线OA是∠BON的角平分线,
∴∠NOA=$\frac{1}{2}$∠NOB,
∵|m-40|+(n-30)2=0,
∴m=40,n=30,
∴∠BON=140°,∠NOC=30°,
∴∠NOA=70°,
∴∠AOC=70°-30°=40°.
点评 本题考查了方向角,余角、补角的定义,根据题意结合角平分线的性质得出∠NOA=$\frac{1}{2}$∠NOB是解决(2)题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
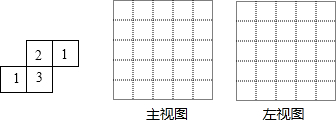
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
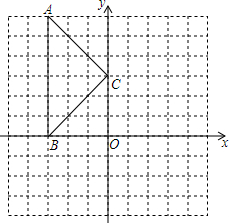 如图,将△ABC放于平面直角坐标系中,得到顶点坐标为A(-3,6),B(-3,0),C(0,3).以B为旋转中心,在平面直角坐标系内将△ABC顺时针旋转90°.
如图,将△ABC放于平面直角坐标系中,得到顶点坐标为A(-3,6),B(-3,0),C(0,3).以B为旋转中心,在平面直角坐标系内将△ABC顺时针旋转90°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
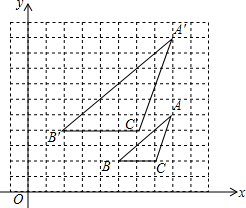 如图,在平面直角坐标系xOy中,△ABC与△A′B′C′顶点的横、纵坐标都是整数.若△ABC与△A′B′C′是位似图形,则位似中心的坐标是(8,0).
如图,在平面直角坐标系xOy中,△ABC与△A′B′C′顶点的横、纵坐标都是整数.若△ABC与△A′B′C′是位似图形,则位似中心的坐标是(8,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
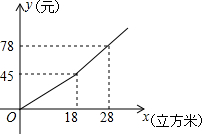 我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com