
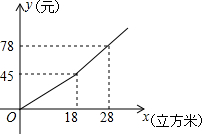
 我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.分析 (1)根据所给出的图象,分两种情况,当0≤x<18时和x≥18时,设出相应的关系式,再代入进行计算即可得出在不同范围内的函数解析式;
(2)根据在不同范围内的函数的解析式可知,在0≤x<18范围内,每立方米2.5元,当x≥18时,每立方米水3.3元;
(3)根据已知条件可知:该用户的交水费范围属于x≥18的范围,代入解析式即可得到答案.
解答 解:(1)当0≤x<18时,设y=k1x,
把点(18,45)代入y=k1x得:45=18k1,
解得:y=2.5x;
当x≥18时,设y=k2x+b,
把点(18,45)和(28,78)代入y=k2x+b得:
$\left\{\begin{array}{l}{45=18{k}_{2}+b}\\{78=28{k}_{2}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=3.3}\\{b=-14.4}\end{array}\right.$,
则y=3.3x-14.4;
(2)根据(1)中得到的函数的解析式可知:
当0≤x<18时,每立方米的水费是2.5元;
当x≥18时,每立方米的水费是3.3元;
(3)把y=51.6代入y=3.3x-14.4得:
51.6=3.3x-14.4,
解得:x=20.
答:这个月最多可用20立方米水.
点评 本题主要考查了一次函数的实际应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
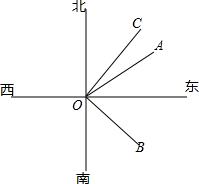 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°.
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com