
 如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2.回答下列问题:
如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2.回答下列问题:分析 (1)根据抛物线的移动规律左加右减可直接得出抛物线y2的解析式,再根据y2的解析式求出顶点坐标即可;
(2)根据阴影部分的面积等于底×高,列式计算即可;
(3)先求出二次函数旋转后的开口方向和顶点坐标,从而得出抛物线y3的解析式.
解答 解:(1)∵抛物线y1=-x2+2向右平移1个单位得到的抛物线y2,
∴抛物线y2的解析式是y2=-(x-1)2+2,顶点坐标为(1,2).
故答案为:y2=-(x-1)2+2,(1,2);
(2)阴影部分的面积是:1×2=2.
故答案为:2;
(3)∵将抛物线y2绕原点O旋转180°后,得到抛物线y3的顶点坐标为:(-1,-2),
∴抛物线y3的解析式为y3=(x+1)2-2,开口方向向上.
故答案为:y3=(x+1)2-2,向上,(-1,-2).
点评 此题考查了二次函数的图象与几何变化,用到的知识点是二次函数的图象和性质、顶点坐标,关键是掌握二次函数的移动规律和几何变换.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
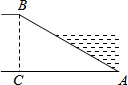 如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )| A. | 9m | B. | 6m | C. | 6$\sqrt{3}$m | D. | 3$\sqrt{3}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
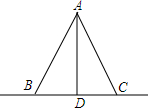 如图所示,用两根钢索加固直立的电线杆,若要使钢索AB与AC的长度相等,需添条件BD=CD,理由是线段垂直平分线上的点到线段两端点的距离相等.
如图所示,用两根钢索加固直立的电线杆,若要使钢索AB与AC的长度相等,需添条件BD=CD,理由是线段垂直平分线上的点到线段两端点的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com