
���� ��1�����ȸ���$\frac{AC}{CB}$=$\frac{m}{n}$=$\frac{2}{3}$���ɵ�AC=$\frac{2}{2+3}��a=\frac{2}{5}a$��Ȼ����AB�ij��ȼ�ȥAC�ij��ȣ����CB�ij����Ƕ��٣������AM�ij��ȼ�ȥAC�ij��ȣ����MC�ij����Ƕ��ټ��ɣ�
��2������C���߶�AB��ʱ���������AC=$\frac{ma}{m+n}$��CB=$\frac{na}{m+n}$��Ȼ�������������ٵ���C��A��M֮��ʱ���ڵ���C��M��B֮��ʱ���ֱ����MC�ij��ȸ��Ƕ��ټ��ɣ�
��3���������⣬������������ٵ���C���߶�AB���ӳ�����ʱ���ڵ���C���߶�AB�ķ����ӳ�����ʱ�����AC��CB��MC�ij����Ƕ��ټ��ɣ�
��� �⣺��1����$\frac{AC}{CB}$=$\frac{m}{n}$=$\frac{2}{3}$��
��AC=$\frac{2}{2+3}��a=\frac{2}{5}a$��
��CB=a-$\frac{2}{5}$a=$\frac{3}{5}$a��
��MC=$\frac{a}{2}-\frac{2}{5}a=\frac{1}{10}a$��
��2������C���߶�AB��ʱ��
AC=$\frac{ma}{m+n}$��CB=$\frac{na}{m+n}$��
�ٵ���C��A��M֮��ʱ��
MC=$\frac{a}{2}-$$\frac{ma}{m+n}$=$\frac{��n-m��a}{2��m+n��}$��
�ڵ���C��M��B֮��ʱ��
MC$\frac{ma}{m+n}$-$\frac{a}{2}$=$\frac{��m-n��a}{2��m+n��}$��
��3������ͼ1�� ��
��
��$\frac{AC}{CB}$=$\frac{m}{n}$��
��$\frac{AC}{AB}=\frac{m}{m-n}$��
��AC=$\frac{am}{m-n}$��
��$\frac{AC}{CB}$=$\frac{m}{n}$��
��$\frac{AB}{CB}=\frac{m-n}{n}$��
��CB=$\frac{an}{m-n}$��
��MC=$\frac{a}{2}+\frac{an}{m-n}$=$\frac{a��m+n��}{2��m-n��}$��
����ͼ2�� ��
��
��$\frac{AC}{CB}$=$\frac{m}{n}$��
��$\frac{AC}{AB}=\frac{m}{n-m}$��
��AC=$\frac{am}{n-m}$��
��$\frac{AC}{CB}$=$\frac{m}{n}$��
��$\frac{AB}{CB}=\frac{n-m}{n}$��
��CB=$\frac{an}{n-m}$��
��MC=$\frac{a}{2}+\frac{am}{n-m}=\frac{a��m+n��}{2��n-m��}$��
�ʴ�Ϊ��$\frac{2}{5}a$��$\frac{3}{5}a$��$\frac{1}{10}a$��$\frac{am}{m-n}$����$\frac{am}{n-m}$����$\frac{an}{m-n}$����$\frac{an}{n-m}$����$\frac{a��m+n��}{2��m-n��}$����$\frac{a��m+n��}{2��n-m��}$����
���� ������Ҫ�����������ľ������Ҫ�������գ�������Ĺؼ���Ū��������߶εij���֮��Ĺ�ϵ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����������ȣ������������ǶԶ��� | |
| B�� | �����εĽ�ƽ������һ������ | |
| C�� | ��Ϊ�ڲ��ǵ���������� | |
| D�� | ͬ�ǵ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ��߽���ֱ������Խ��ߵ��е� | |
| B�� | һ��Ա�ƽ�У�һ��Խ���� | |
| C�� | һ��Ա���ȣ�һ���Խ��߱���һ���Խ���ƽ�� | |
| D�� | һ��Ա�ƽ�У�һ���Խ��߱���һ���Խ���ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
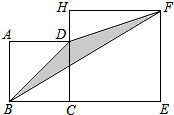 ��ͼ��������ABCD�ı߳�Ϊ2��H��CD���ӳ����ϣ��ı���CEFHҲΪ�����Σ����DBF�����Ϊ2��
��ͼ��������ABCD�ı߳�Ϊ2��H��CD���ӳ����ϣ��ı���CEFHҲΪ�����Σ����DBF�����Ϊ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
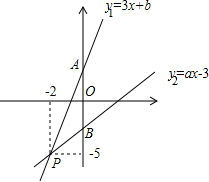 ��ͼ����֪����y1=3x+b��y2=ax-3��ͼ���ڵ�P��-2��-5������ʽ3x+b��ax-3�Ľ⼯Ϊ��������
��ͼ����֪����y1=3x+b��y2=ax-3��ͼ���ڵ�P��-2��-5������ʽ3x+b��ax-3�Ľ⼯Ϊ��������| A�� | x��-2 | B�� | x��-2 | C�� | x��-5 | D�� | x��-5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ���ı���ABCD��ƽ���ı��Σ���֤��ƽ���ı��ε�����Ա߷ֱ���ȣ�
��֪����ͼ���ı���ABCD��ƽ���ı��Σ���֤��ƽ���ı��ε�����Ա߷ֱ���ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com