
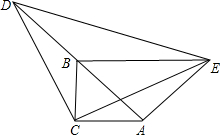
 如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
|
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,AC=10,BC=30,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿边CA向点A以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=10,BC=30,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿边CA向点A以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:
 在活动课上,小明和小红合作用一副三角板来测量学校旗杆MN的高度,在旗杆一侧的地面上,小明按如图所示的方式放置含45°的三角板,并调整其位置,使斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M的仰角为45°,在旗杆另一侧的地面上,小红用同样的方法测得旗杆顶端M的仰角为30°,此时,两人相距28m,且点A,N,B在同一条直线上,请你求出旗杆MN的高度(参考数据:
在活动课上,小明和小红合作用一副三角板来测量学校旗杆MN的高度,在旗杆一侧的地面上,小明按如图所示的方式放置含45°的三角板,并调整其位置,使斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M的仰角为45°,在旗杆另一侧的地面上,小红用同样的方法测得旗杆顶端M的仰角为30°,此时,两人相距28m,且点A,N,B在同一条直线上,请你求出旗杆MN的高度(参考数据:| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com