
【题目】在平面直角坐标系中,直线l1:y=﹣2x+6与坐标轴交于A,B两点,直线l2:y=kx+2(k>0)与坐标轴交于点C,D,直线l1,l2与相交于点E.
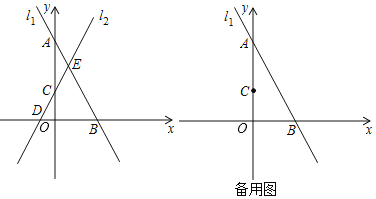
(1)当k=2时,求两条直线与x轴围成的△BDE的面积;
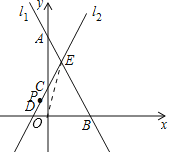
(2)点P(a,b)在直线l2:y=kx+2(k>0)上,且点P在第二象限.当四边形OBEC的面积为![]() 时.
时.
①求k的值;
②若m=a+b,求m的取值范围.
【答案】(1)△BDE的面积=8;(2)①k=4;②﹣![]() <m<2.
<m<2.
【解析】
(1)由直线l1的解析式可得点A、点B的坐标,当k=2时,由直线l2的解析式可得点C、点D坐标,联立直线l1与直线l2的解析式可得点E坐标,根据三角形面积公式求解即可;
(2)①连接OE.设E(n,﹣2n+6),由S四边形OBEC=S△EOC+S△EOB可求得n的值,求出点E坐标,把点E代入y=kx+2中求出k值即可;②由直线y=4x+2的表达式可确定点D坐标,根据点P(a,b)在直线y=4x+2上,且点P在第二象限可得![]() 及
及![]() 的取值范围,由m=a+b可确定m的取值范围.
的取值范围,由m=a+b可确定m的取值范围.
解:(1)∵直线l1:y=﹣2x+6与坐标轴交于A,B两点,
∴当y=0时,得x=3,当x=0时,y=6;
∴A(0,6)B(3,0);
当k=2时,直线l2:y=2x+2(k≠0),
∴C(0,2),D(﹣1,0)
解![]() 得
得![]() ,
,
∴E(1,4),
![]() ,点E到x轴的距离为4,
,点E到x轴的距离为4,
∴△BDE的面积=![]() ×4×4=8.
×4×4=8.
(2)①连接OE.设E(n,﹣2n+6),
∵S四边形OBEC=S△EOC+S△EOB,
∴![]() ×2×n+
×2×n+![]() ×3×(﹣2n+6)=
×3×(﹣2n+6)=![]() ,
,
解得n=![]() ,
,
∴E(![]() ,
,![]() ),
),
把点E代入y=kx+2中,![]() =
=![]() k+2,
k+2,
解得k=4.
②∵直线y=4x+2交x轴于D,
∴D(﹣![]() ,0),
,0),
∵P(a,b)在第二象限,即在线段CD上,
∴﹣![]() <a<0,
<a<0,
∵点P(a,b)在直线y=kx+2上
∴b=4a+2,
∴m=a+b=5a+2,
![]()
∴﹣![]() <m<2.
<m<2.


科目:初中数学 来源: 题型:
【题目】从6 月30日起,某县普降特大暴雨,遭受了短期降水量最大、内河水位历史最高、防汛压力最重的百年不遇的灾害.洪水无情人有情,该县实验学校9 (1)班计划用捐款从商店购买同品牌的雨衣和雨伞送往抗洪前线.已知购买一件雨衣比购买一把雨伞多用![]() 元,若用
元,若用![]() 元购买雨衣和用
元购买雨衣和用![]() 元购买雨伞,则购买雨衣的件数是购买雨伞把数的一半.
元购买雨伞,则购买雨衣的件数是购买雨伞把数的一半.
(1)求购买该品牌的一件雨衣、一把雨伞各需要多少元.
(2)经商谈,商店给予该班级购买一件该品牌的雨衣赠送把该品牌的雨伞的优惠, 如果该班需要购买雨伞个数是雨衣件数的![]() 倍还多
倍还多![]() 个,且该班购买雨衣和雨伞的总费用不超过
个,且该班购买雨衣和雨伞的总费用不超过![]() 元,那么该班最多可以购买多少件该品牌的雨衣?
元,那么该班最多可以购买多少件该品牌的雨衣?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() , 点
, 点![]() 在
在![]() 边上,点
边上,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等.
的距离相等.

(1)利用尺规作图作出点![]() ,不写作法但保留作图痕迹:
,不写作法但保留作图痕迹:
(2)连接![]() ,若
,若![]() 的底边长为
的底边长为![]() ,周长为
,周长为![]() ,求
,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;
(2)求圆O的半径长.
(本题参考数据:sin 67.4° =![]() ,cos 67.4°=
,cos 67.4°=![]() ,tan 67.4° =
,tan 67.4° =![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是圆
是圆![]() 的直径,
的直径,![]() ,点
,点![]() 是圆
是圆![]() 上一动点(与
上一动点(与![]() ,
,![]() 不重合),
不重合),![]() 的平分线交圆
的平分线交圆![]() 于
于![]() .
.
![]() 判断
判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
![]() 若
若![]() 是
是![]() 的内心,当点
的内心,当点![]() 运动时,
运动时,![]() 、
、![]() 中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.
中是否存在长度保持不变的线段?如果存在,请指出并求其长度;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1:y1=x+b经过点A(﹣5,0),交y轴于点B,直线l2:y2=﹣2x﹣4与直线l1:y1=x+b交于点C,交y轴于点D.
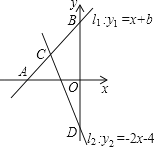
(1)求b的值;
(2)求△BCD的面积;
(3)当0≤y2<y1时,则x的取值范围是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,李老师让同学们试着用角尺平分 ![]() (如图所示),有两组.
(如图所示),有两组.
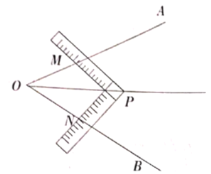
同学设计了如下方案:
方案①:将角尺的直角顶点![]() 介于射线
介于射线![]() 之间,移动角尺使角尺两边相同的刻度位于
之间,移动角尺使角尺两边相同的刻度位于![]() 上,且交点分别为
上,且交点分别为![]() ,即
,即![]() ,过角尺顶点
,过角尺顶点![]() 的射线
的射线![]() 就是
就是![]() 的平分线.
的平分线.
方案②:在边![]() 上分别截取
上分别截取![]() ,将角尺的直角顶点
,将角尺的直角顶点![]() 介于射线
介于射线![]() 之间,移动角尺使角尺两边相同的刻度与点
之间,移动角尺使角尺两边相同的刻度与点![]() 重合,即
重合,即![]() ,过角尺顶点
,过角尺顶点![]() 的射线
的射线![]() 就是
就是![]() 的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com