
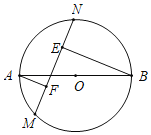
【题目】如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离分别为h1,h2,则|h1﹣h2|等于_____.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆心为P(![]() ,
,![]() )的动圆经过点A(1,2)且与
)的动圆经过点A(1,2)且与![]() 轴相切于点B.
轴相切于点B.
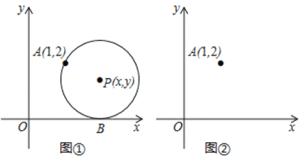
(1)当![]() =2是,求⊙P的半径;
=2是,求⊙P的半径;
(2)求![]() 关于
关于![]() 的函数解析式,在图②中画出此函数图像;
的函数解析式,在图②中画出此函数图像;
(3)请类比圆的定义(圆可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图像进行定义:此函数图像可以看成是到 的距离等于到 的距离的所有点的集合;
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(![]() ,
,![]() )在点C的右侧,请利用图②,则cos∠APD= .
)在点C的右侧,请利用图②,则cos∠APD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OA1B1C1的边长为1,以O为圆心,OA1为半径作扇形OA1C1,弧A1C1与OB1相交于点B2,设正方形OA1B1C1与扇形OA1C1之间的阴影部分的面积为S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心,OA2为半径作扇形OA2C2,弧A2C2与OB1相交于点B3,设正方形OA2B2C2与扇形OA2C2之间的阴影部分面积为S2;按此规律继续作下去,设正方形OA2018B2018C2018与扇形OA2018C2018之间的阴影部分面积为S2018,则S2018=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列尺规作图中,能确定圆心的是( )
①如图1,在圆上任取三个点A,B,C,分别作弦AB,BC的垂直平分线,交点O即为圆心
②如图2,在圆上任取一点B,以B为圆心,小于直径长为半径画弧交圆于A,C两点连结AB,BC,作∠ABC的平分线交圆于点D,作弦BD的垂直平分线交BD于点O,点O即为圆心
③如图3,在圆上截取弦AB=CD,连结AB,BC,CD,分别作∠ABC与∠DCB的平分线,交点O即为圆心

A. ①②B. ①③C. ②④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
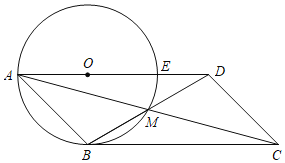
【题目】平行四边形ABCD的对角线相交于点M,△ABM的外接圆交AD于点E且圆心O恰好落在AD边上,连接ME,若∠BCD=45°
(1)求证:BC为⊙O切线;
(2)求∠ADB的度数;
(3)若ME=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,顶点为D.
(1)求此抛物线的函数表达式;
(2)以点B为直角顶点作直角三角形BCE,斜边CE与抛物线交于点P,且CP=EP,求点P的坐标;
(3)△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转的角度为α,旋转后的图形为△BO1C1.当旋转后的△BO1C1有一边在直线BD上时,求△BO1C1不在BD上的顶点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一个月以每件100元的价格购进200件衬衫,以每件150元的价格售罄.由于市场火爆,该商店第二个月再次购进一批衬衫,与第一批衬衫相比,这批衬衫的进价和数量都有一定的提高,其数量的增长率是进价增长率的2.5倍,该批衬衫仍以每件150元销售.第二个月结束后,商店对剩余的50件衬衫以每件120元的价格一次性清仓销售,商店出售这两批衬衫共盈利17500元.设第二批衬衫进价的增长率为x.
(1)第二批衬衫进价为 元,购进的数量为 件.(都用含x的代数式表示,不需化简)
(2)求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
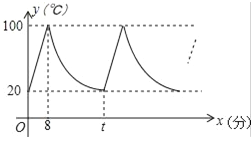
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBD是等腰三角形,EB=ED;②折叠后∠ABE和∠CBD一定相等;③折叠后得到的图形是轴对称图形;④△EBA和△EDC一定是全等三角形.其中正确的是( )

A. ①②③B. ①③④C. ①②④D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com