
【题目】如图①,已知抛物线y=﹣x2﹣2x+3与x轴交于点A和点B,与y轴交于点C.
(1)直接写出A,B,C三点的坐标:A ;B ;C ;
(2)在该抛物线的对称轴上是否存在点P,时△APC的周长最小,若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图②,若点E为第二象限抛物线上的一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.

【答案】(1)A(1,0);B(﹣3,0);C(0,3);(2)存在.(3)点E坐标为(![]() ).
).
【解析】试题分析:
(1)在y=﹣x2﹣2x+3中分别由y=0和x=0求出对应的x的值和y的值即可得到A、B、C三点的坐标;
(2)由已知易得抛物线y=﹣x2﹣2x+3的对称轴为直线x=1,由题意可知点A、B关于直线x=1对称,连接BC交直线x=1于点P,则此时△ACP的周长最小,由点B、C的坐标可求出直线BC的解析式,把x=1代入所求解析式中求得对应的y的值即可得到点P的坐标;
(3)如图2,连接OE,由题意可设点E的坐标为(a,﹣a2﹣2a+3)(﹣3<a<0),由S四边形BOCE=S△OBE+S△OCE即可列式表达出其面积,将所得表达式配方,结合二次函数的性质即可得到四边形BOCE面积的最大值和对应的点E的坐标.
试题解析:
(1)令x=0得:y=3,
∴C(0,3).
令y=0,则0=﹣x2﹣2x+3,解得:x=﹣3或x=1,
∴A(1,0),B(﹣3,0).
故答案为:A(1,0);B(﹣3,0);C(0,3).
(2)存在.
如图①所示:连接BC,交抛物线的对称轴与点P,连接PA.
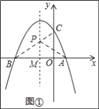
由题意可知,A、B两点关于抛物线的对称轴x=﹣1对称
∴PB=PA.
∴PC+PA=PC+PB.
由两点之间线段最短可知:PC+PA有最小值.
∴此时△APC周长最小.
设直线BC的解析式为y=kx+b.
将点B和点C的坐标代入得: ![]() ,解得k=1,b=3.
,解得k=1,b=3.
∴直线BC的解析式为y=x+3.
把x=﹣1代入y=x+3得y=2
∴P(﹣1,2)
(3)如图②所示:连接OE.
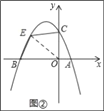
设E(a,﹣a2﹣2a+3)(﹣3<a<0).
S四边形BOCE=![]() OB|yE|+
OB|yE|+![]() OC|xE|=
OC|xE|=![]() ×3×(﹣a)+
×3×(﹣a)+![]() ×3×(﹣a2﹣2a+3)=﹣
×3×(﹣a2﹣2a+3)=﹣![]() a2﹣
a2﹣![]() a+
a+![]() =﹣
=﹣![]() (a+
(a+![]() )2+
)2+![]() .
.
∴当a=﹣![]() 时,四边形BOCE面积最大,且最大面积为
时,四边形BOCE面积最大,且最大面积为![]() .
.
此时,点E坐标为(![]() ).
).


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使BC边与三角形ADE的一边互相平行.则∠BAD(0°<∠BAD<180°)所有可能符合条件的度数为________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象
的图象![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点,正比例函数的图象
两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]()

(1)求![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图象为
的图象为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级A班有50人,某次活动中分为四组,第一组有3a+4b+2人第二组比第一组的一半多b人,第三组比前两组的和的![]() 多3人.
多3人.
(1)求第四组的人数(用含a,b的整式表示)
(2)试判断a=1,b=2时,是否满足题意
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足(a-![]() )2+
)2+![]() +
+![]() =0,
=0,
(1)求a、b、c的值.
(2)试问以a、b、c为边能否构成直角三角形?若能构成,求出直角三角形周长;若不能构成直角三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
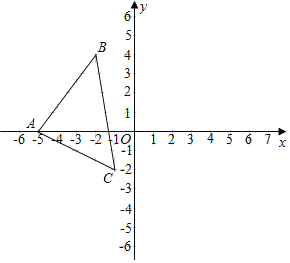
【题目】△ABC三顶点A(﹣5,0)、B(﹣2,4)、C(﹣1,﹣2),△A'B'C'与△ABC关于y轴对称.
(1)直接写出A'、B'、C'的坐标;
(2)画出△A'B'C';
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)若小亮一年内来此游泳馆的次数为15次,选择哪种方式比较划算?
(3)若小亮计划拿出1400元用于在此游泳馆游泳,采用哪种付费方式更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
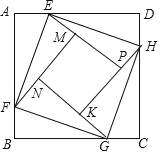
【题目】如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
A. 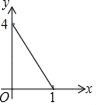 B.
B. 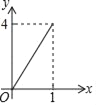 C.
C.  D.
D. 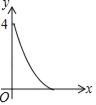
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com