
分析 先根据坐标轴上点的坐标特征确定直线y=kx+1与x轴的交点坐标为(-$\frac{1}{k}$,0),与y轴的交点坐标为(0,1),再根据三角形面积公式得到$\frac{1}{2}$×1×|-$\frac{1}{k}$|=2,然后解方程即可.
解答 解:把x=0代入y=kx+1得k=1;把y=0代入y=kx+1得kx+1=0,解得x=-$\frac{1}{k}$,
所以直线y=kx+1与x轴的交点坐标为(-$\frac{1}{k}$,0),与y轴的交点坐标为(0,1),
所以$\frac{1}{2}$×1×|-$\frac{1}{k}$|=2,
解得k=±$\frac{1}{4}$.
点评 本题考查了一次函数图象上点的坐标,关键是根据坐标轴上点的坐标特征确定直线y=kx+1与x轴的交点坐标.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
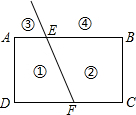 如图,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区城③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).
如图,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区城③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
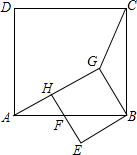 如图,在Rt△AGB中,∠AGB=90°,∠GAB=30°,以GB为边在GB的下方作正方形GBEH,以AB为边在AB的上方作正方形ABCD,连结CG.若FB=2,则CG2的值为15-6$\sqrt{3}$.
如图,在Rt△AGB中,∠AGB=90°,∠GAB=30°,以GB为边在GB的下方作正方形GBEH,以AB为边在AB的上方作正方形ABCD,连结CG.若FB=2,则CG2的值为15-6$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com