
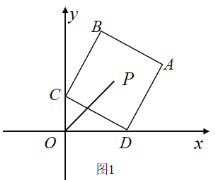
【题目】如图,在平面直角坐标系中,![]() 点的坐标是
点的坐标是![]() .图1中,点
.图1中,点![]() 为正方形
为正方形![]() 的对称中心,顶点
的对称中心,顶点![]() 分别在
分别在![]() 轴和
轴和![]() 轴的正半轴上,则
轴的正半轴上,则![]() ___ 图2中,点
___ 图2中,点![]() 为正
为正![]() 的重心,顶点
的重心,顶点![]() 分别在
分别在![]() 轴和
轴和![]() 轴的正半轴上,则
轴的正半轴上,则![]() ___________.
___________.

【答案】![]()
![]()
【解析】
作AM⊥x轴于点M,证明△ADM≌△DCO,得出C点坐标,根据中点坐标求出点P坐标,运用勾股定理求出OP的长;通过证明△BHD∽△AGD,△DPQ∽△DBH,△DPQ∽△DAG,求出相应线段的长度,得到点P的坐标,运用勾股定理即可得到OP的长.
如图,作AM⊥x轴于点M,
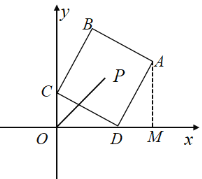
∵四边形ABCD是正方形,
∴∠ADC=90°
![]()
∵![]()
![]()
又CD=AD
∴△ADM≌△DCO
∴CO=DM,OD=AM,
∵A(4,3)
∴AM=3,OM=4,
∴DM=OM-OD=OM-AM=4-3=1,
∴OC=DM,
即C(0,1)
∵点![]() 为正方形
为正方形![]() 的对称中心,
的对称中心,
∴P(![]() ,
,![]() ),即P(2,2)
),即P(2,2)
∴![]() ;
;
(2)过B点作BD⊥AC于点D,
∵△ABC是正三角形,P为重心,
∴P在AD上,
过A点作AE⊥x轴于点E,
过D作DH//x轴,交AE、y轴分别为G、H,
过P作PQ⊥HG于点Q,
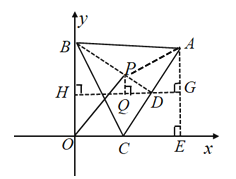
∵D为AC的中点,DG//x轴,
∴DG=![]() CE,AG=
CE,AG=![]() AE=
AE=![]() ,
,
又∵∠BDA=90°,
∴∠BDH+∠ADG=90°,
∵∠DAG+∠ADG=90°,
∴∠BDH=∠DAG,
又∠BHD=∠AGD=90°
∴△BHD∽△AGD
∴![]()
∵![]()
∴![]()
∴![]() ,
,![]()
连接AP,则∠PAD=30°,
∴![]()
∵PQ⊥HG,BH⊥HG,
∴PG//BH
∴△DPQ∽△DBH
∴△DPQ∽△DAG,
∴![]() ,
,
∴![]() ,
,![]()
∴点P的纵坐标为:PQ+GE=![]() ,横坐标为:
,横坐标为:![]()
∴P(![]() ,
,![]() ),
),
∴![]() .
.
故答案为:![]() ;
;![]() .
.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
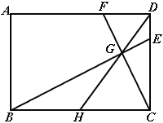
【题目】如图,在矩形ABCD中,点H为边BC的中点,点G为线段DH上一点,且∠BGC=90°,延长BG交CD于点E,延长CG交AD于点F,当CD=4,DE=1时,则DF的长为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是菱形,
是菱形,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,设点
,设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
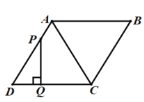
的面积为![]() ,则下列图象能正确反映
,则下列图象能正确反映![]() 与
与![]() 之间的函数关系的是( ).
之间的函数关系的是( ).
A.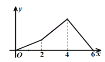 B.
B.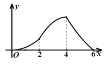 C.
C.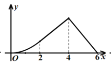 D.
D.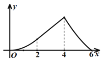
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB//CD,直线EF交AB于点E,交CD于点F,EP平分∠AEF,FP平分∠CFE,∠BEP=α,∠DFP=β,则a+β=( )

A.180°B.225°C.270°D.315°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经销商购进某种商品,当购进量在20千克~50千克之间(含20千克和50千克)时,每千克进价是5元;当购进量超过50千克时,每千克进价是4元.此种商品的日销售量y(千克)受销售价x(元/千克)的影响较大,该经销商试销一周后获得如下数据:
x(元/千克) | 5 | 5.5 | 6 | 6.5 | 7 |
y(千克) | 90 | 75 | 60 | 45 | 30 |
解答下列问题:
(1)求出y关于x的一次函数表达式:
(2)若每天购进的商品能够全部销售完,且当日销售价不变,日销售利润为w元,那么销售价定为多少时,该经销商销售此种商品的当日利润最大?最大利润为多少元?此时购进量应为多少千克?(注:当日利润=(销售价-进货价)×日销售量).
查看答案和解析>>
科目:初中数学 来源: 题型:
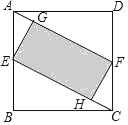
【题目】如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=3![]() x2 B. y=4
x2 B. y=4![]() x2 C. y=8x2 D. y=9x2
x2 C. y=8x2 D. y=9x2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com