
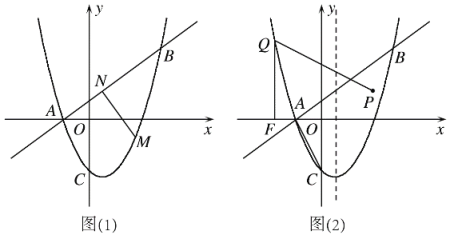
����Ŀ����ͼ��������y��x2��bx��c��x�ύ��A����1��0������y�ύ��C��0����2����ֱ��![]() ������A���������߽�����һ��B
������A���������߽�����һ��B![]() ��
��
��1��ֱ��д�������ߵĽ���ʽ ��
��2����ͼ��1������M����������A��B��������һ���㣬MN��AB�ڵ�N�������MN�����ֵ �������MN���ʱ��M�����ꣻ
��3����ͼ��2��������AC����֪��P������Ϊ��2��1������QΪ�Գ��������������ϵ�һ���㣬����Q��QF��x���ڵ�F���Ƿ���������ĵ�Q��ʹ�á�FQP����CAO�������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��x2��x��2 ����2��![]() ��M��
��M��![]() ��
��![]() ������3�����ڣ���
������3�����ڣ���![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������
��1����A��C�����������y��x2��bx��c���b��c��ֵ���ɣ�
��2������M��ME��x���ڵ�D����AB�ڵ�E����M(m��m2��m��2)����E(m��![]() m��
m��![]() ),�����ME����m2��
),�����ME����m2��![]() m��
m��![]() ��֤����AED�ס�MEN��MN����
��֤����AED�ס�MEN��MN����![]() m2��
m2��![]() m��
m��![]() �����ö��κ��������ʿɵý��ۣ�
�����ö��κ��������ʿɵý��ۣ�
��3����Q������λ�ã�ʹ�á�FQP����CAO���ֱ������ʱPQ�Ľ���ʽ���������߷������������飬���������Ľ⼴ΪQ�������.
�⣺��1����A��-1,0����C��0��-2����������е�
![]() �����
�����![]()
�������ߵĽ���ʽΪy��x2��x��2��
��2����ͼ������M��ME��x���ڵ�D����AB�ڵ�E.
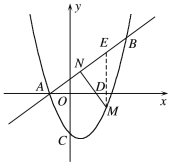
��M(m��m2��m��2) (��1��m��![]() )��
)��
��E(m��![]() m��
m��![]() ),
),
ME��(![]() m��
m��![]() )��(m2��m��2)����m2��
)��(m2��m��2)����m2��![]() m��
m��![]() .
.
�ڡ�AED���MEN�У���AED����MEN����ADE����MNE��
���AED�ס�MEN��
��![]() ��
��
��MN��![]() ME��
ME��![]() (��m2��
(��m2��![]() m��
m��![]() )����
)����![]() m2��
m2��![]() m��
m��![]() (��1��m��
(��1��m��![]() )��
)��
�൱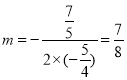 ʱ��MN���Ϊ
ʱ��MN���Ϊ![]() ��
��
��ʱM��![]() ��
��![]() ��.
��.
��3�����ڣ�
������֪�������ߵĶԳ���Ϊֱ��![]() ��
��
����P��PG��y���ڵ�G������OP��
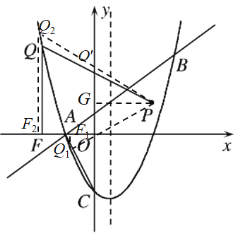
������OG��OA��1��PG��OC��2����PGO����COA��90�㣬
���PGO�ա�COA��
���POG����CAO��
�ӳ�PO���������ڵ�Q1����Q1��Q1F1��x���ڵ�F1��
��ʱ��F1Q1P����POG����CAO.
��ֱ֪��OP�Ľ���ʽΪ![]() ,
,
��![]() ��
��
���![]() ��
��![]() ����ȥ����
����ȥ����
��![]() .
.
ͬ������y������һ��O�䣬ʹO��G��OG��1��
����֤����PGO��ա�COA��
���PO��G����CAO��
�ӳ�PO�佻�������ڵ�Q2��
����Q2��Q2F2��x���ڵ�F2��
��ʱ����F2Q2P����PO��G����CAO.
��ֱ֪��O��P�Ľ���ʽΪ![]() ��
��
��![]() ��
��
���![]() ��
��![]() ����ȥ����
����ȥ����
��![]() .
.
���Q��������![]() ��
��![]() ����
����![]() ��
��![]() ��.
��.


 ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����κ���y1��x2+bx+a��y2��ax2+bx+1��a��b��ʵ����a��0����
��1��������y1�ĶԳ���Ϊֱ��x��3���Һ���y1��ͼ���㣨a��b��������y1�ı���ʽ��
��2��������y1��ͼ���㣨r��0��������r��0����֤������y2��ͼ���㣨![]() ��0����
��0����
��3���躯��y1�ͺ���y2����Сֵ�ֱ�Ϊm��n����m+n��0����m��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
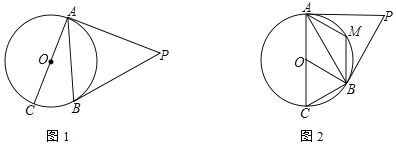
����Ŀ����ͼ��AC����O��ֱ����PA��PB����O�����ߣ��е�ֱ��ǵ�A��B
��1����ͼ1������BAC=25�㣬���P�Ķ�����
��2����ͼ2����M���ӻ�AB��һ�㣬��AMB=��AOB�����P�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ��ֱ��
��ֱ��![]() ƽ����
ƽ����![]() �ᣬ����������һ������Ϊ
�ᣬ����������һ������Ϊ![]() ��
��
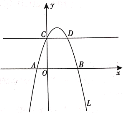
��1����������![]() �ĺ�������ʽ����D�����ꣻ
�ĺ�������ʽ����D�����ꣻ
��2����������![]() ��������
��������![]() ����
����![]() ��Գƣ�
��Գƣ�![]() ��
��![]() ���ϵĶ��㣬��������
���ϵĶ��㣬��������![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ����
��ʹ����![]() Ϊ������
Ϊ������![]() Ϊ�ߵ��ı�����ƽ���ı��Σ������ڣ��������
Ϊ�ߵ��ı�����ƽ���ı��Σ������ڣ��������![]() �����꣬�������ڣ���˵������.
�����꣬�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
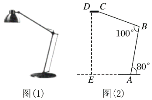
����Ŀ����ͼ��1����С���ҹ����һ��̨�ƣ��ֺ���֧�ܵĴ�ϸ���õ����IJ����ʾ��ͼ��ͼ��2����ʾ��֧��AB������ļн�Ϊ80�㣬֧��AB��֧��BC�ļн�Ϊ100�㣬CDƽ�������棬֧��AB��BC�ij��Ⱦ�Ϊ20cm������ݶ���D������ľ���DE���������ȷ��1cm���ο����ݣ�sin80���0.98��cos80���0.17��tan80���5.67��sin20���0.34��cos20���0.94��tan20���0.36��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
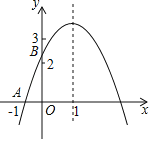
����Ŀ����ͼ�����κ���y��ax2+bx+c��a��0��ͼ����x�ύ��A����1��0�����Գ���Ϊֱ��x��1����y��Ľ���B�ڣ�0��2���ͣ�0��3��֮�䣨�������������㣩�����н��ۣ�
�ٵ���1��x��3ʱ��y��0���ک�1��a����![]() ���۵�m��1ʱ��a+b��m��am+b������4ac��b2��8a������ȷ�Ľ�����_____��
���۵�m��1ʱ��a+b��m��am+b������4ac��b2��8a������ȷ�Ľ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��![]() �Ϸ���һ��������
�Ϸ���һ��������![]() ��
��![]() ���Ե�
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��������
Ϊ�뾶��������![]() ���ڵ�
���ڵ�![]() ���ֱ��Ե�
���ֱ��Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶�������������ڵ�
��Ϊ�뾶�������������ڵ�![]() ������
������![]() ����
����![]() �Ķ���Ϊ______.
�Ķ���Ϊ______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڱ�������Ʒ������ʡũ��Ժ���Ƶ�������Ʒ�֣�����ʡ���㷺��ֲ��������ij������ֲ����2017����ֲ����ڱ���100Ķ����2019�ꡰ�ڱ�������ֲ����ﵽ196Ķ.
��1����û��������ꡰ��ڱ�����ֲ�����ƽ�������ʣ�
��2���г����鷢�֣�������ڱ������ۼ�Ϊ20Ԫ/ǧ��ʱ��ÿ�����۳�200ǧ�ˣ��ۼ�ÿ����1Ԫ��ÿ��ɶ��۳�50ǧ�ˣ�Ϊ���ƹ����������ؾ������۴�����ͬʱ���ٿ�棬��֪�û��ء���ڱ�����ƽ���ɱ���Ϊ12Ԫ/ǧ�ˣ���ʹ���ۡ���ڱ���ÿ�����1750Ԫ�����ۼ�Ӧ���Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
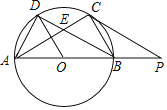
����Ŀ����ͼ��AB�ǡ�O��ֱ������AC��BD���ڵ�E����AC��BD������AD��BC��
��1����֤����ADB�ա�BCA��
��2����OD��AC��AB��4������AC�ij���
��3���ڣ�2���������£��ӳ�AB����P��ʹBP��2������PC����֤��PC�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com