
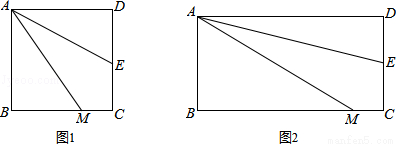
【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
(1)证明见解析;
成立;证明见解析;
(3)①结论AM=AD+MC仍然成立.
②结论AM=DE+BM不成立.
【解析】
试题分析:(1)从平行线和中点这两个条件出发,延长AE、BC交于点N,如图1(1),易证△ADE≌△NCE,从而有AD=CN,只需证明AM=NM即可.
(2)作FA⊥AE交CB的延长线于点F,易证AM=FM,只需证明FB=DE即可;要证FB=DE,只需证明它们所在的两个三角形全等即可.
(3)在图2(1)中,仿照(1)中的证明思路即可证到AM=AD+MC仍然成立;在图2(2)中,采用反证法,并仿照(2)中的证明思路即可证到AM=DE+BM不成立.
试题解析:(1)延长AE、BC交于点N,如图1(1),
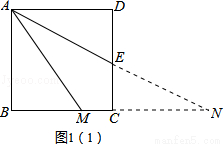
∵四边形ABCD是正方形,
∴AD∥BC.
∴∠DAE=∠ENC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠ENC=∠MAE.
∴MA=MN.
在△ADE和△NCE中,
 ,
,
∴△ADE≌△NCE(AAS).
∴AD=NC.
∴MA=MN=NC+MC=AD+MC.
(2)AM=DE+BM成立.
过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.
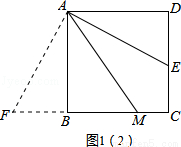
∵四边形ABCD是正方形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.
∵AF⊥AE,
∴∠FAE=90°.
∴∠FAB=90°﹣∠BAE=∠DAE.
在△ABF和△ADE中,
 ,
,
∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM
=∠BAM+∠FAB
=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
(3)①结论AM=AD+MC仍然成立.
延长AE、BC交于点P,如图2(1),
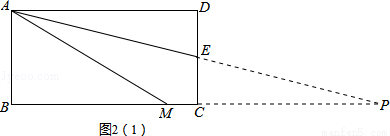
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DAE=∠EPC.
∵AE平分∠DAM,
∴∠DAE=∠MAE.
∴∠EPC=∠MAE.
∴MA=MP.
在△ADE和△PCE中,
 ,
,
∴△ADE≌△PCE(AAS).
∴AD=PC.
∴MA=MP=PC+MC
=AD+MC.
②结论AM=DE+BM不成立.
假设AM=DE+BM成立.
过点A作AQ⊥AE,交CB的延长线于点Q,如图2(2)所示.
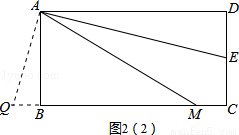
∵四边形ABCD是矩形,
∴∠BAD=∠D=∠ABC=90°,AB∥DC.
∵AQ⊥AE,
∴∠QAE=90°.
∴∠QAB=90°﹣∠BAE=∠DAE.
∴∠Q=90°﹣∠QAB
=90°﹣∠DAE
=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠QAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM
=∠BAM+∠QAB
=∠QAM.
∴∠Q=∠QAM.
∴AM=QM.
∴AM=QB+BM.
∵AM=DE+BM,
∴QB=DE.
在△ABQ和△ADE中,
 ,
,
∴△ABQ≌△ADE(AAS).
∴AB=AD.
与条件“AB≠AD“矛盾,故假设不成立.
∴AM=DE+BM不成立.
考点:1、角平分线的定义;2、平行线的性质;3、全等三角形的判定与性质;4、矩形及正方形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2015届河北省滦南县八年级下学期期中考试数学试卷(解析版) 题型:填空题
已知等腰三角形的周长为24cm,腰长为x(cm),底边为y(cm),则底边y与x的函数关系式为 ,自变量x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2015届河北省唐山市八年级下学期期末考数学试卷(解析版) 题型:选择题
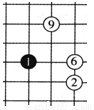
如图1是一局围棋比赛的几手棋.为记录棋谱方便,横线用数字表示,纵线用字母表示,这样,黑棋 的位置可记为(B,2),白棋②的位置可记为(D,1),则白棋⑨的位置应记为( )
的位置可记为(B,2),白棋②的位置可记为(D,1),则白棋⑨的位置应记为( )
A.(C,5) B.(C,4) C.(4,C) D.(5,C)
查看答案和解析>>
科目:初中数学 来源:2015届江西省高安市八年级下学期期末考试数学试卷(解析版) 题型:填空题
若一组数据:7、9、6、x、8、7、5的极差是6,那么x的值是 _________ .
查看答案和解析>>
科目:初中数学 来源:2015届江西省高安市八年级下学期期末考试数学试卷(解析版) 题型:选择题
如图,大正方形中有2个小正方形,如果它们的面积分别是S1、S2,那么S1、S2的大小关系是( )
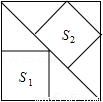
A.S1>S2 B.S1=S2
C.S1<S2 D.S1、S2的大小关系不确定
查看答案和解析>>
科目:初中数学 来源:2015届江西省九年级上学期入学考试数学试卷(解析版) 题型:解答题
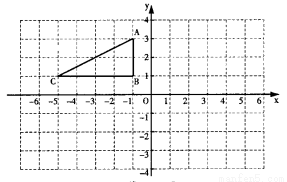
△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移6个单位得到△A1B1C1,请画出△A1B1C1;并写出点C1的坐标;
(2)将△ABC绕原点O旋转180°得到△A2B2C2,请画出△A2B2C2.
查看答案和解析>>
科目:初中数学 来源:2015届江西省八年级下学期第一次月考数学试卷(解析版) 题型:解答题
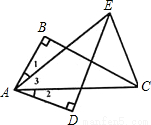
(8分)如图所示,已知∠1=∠2,AB=AD, ∠B=∠D=90º,请判断△AEC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com