
分析 (1)先计算判别式的值,再配方得到△=4(m+1)2+8,则根据非负数的性质可判断△>0,于是根据判别式的意义可判断无论m取何值,该函数图象与x轴总有两个交点;
(2)利用二次函数与x轴的交点问题,x1和x2为方程x2-2mx-2=0的两根,由根与系数的关系得到x1+x2=2m,x1•x2=-2(m+3),再利用$\frac{1}{x_1}$+$\frac{1}{x_2}$=-$\frac{1}{4}$得到$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{4}$,则$\frac{2m}{-2(m+3)}$=-$\frac{1}{4}$,解得m=1,于是得到抛物线解析式为y=x2-2m-8,接着通过解方程x2-2m-8=0得到A(-2,0),B(4,0),利用直线y=x-10得到它与坐标轴的交点为C、E的坐标,如图,则可判断△OCE为等腰直角三角形,得到∠OCE=45°,然后作B点关于CE的对称点D,如图,则∠DCE=∠BCE=45°,所以△BCD为等腰直角三角形,于是可得到D(10,-6),连结AD交CE于M,连结MB,如图,利用两点之间线段最短可判断此时MA+MB最小,最后利用待定系数法可求出直线AM的解析式.
解答 (1)证明:△=(-2m)2-4•[-2(m+3)]
=4m2+8m+12
=4(m+1)2+8,
∵4(m+1)2≥0,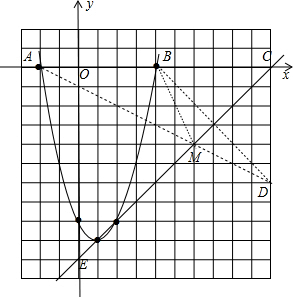
∴4(m+1)2+8>0,即△>0,
∴无论m取何值,该函数图象与x轴总有两个交点;
(2)解:x1和x2为方程x2-2mx-2=0的两根,则x1+x2=2m,x1•x2=-2(m+3),
∵$\frac{1}{x_1}$+$\frac{1}{x_2}$=-$\frac{1}{4}$,
∴$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{4}$,
∴$\frac{2m}{-2(m+3)}$=-$\frac{1}{4}$,解得m=1,
∴抛物线解析式为y=x2-2m-8,
当y=0时,x2-2m-8=0,解得x1=-2,x2=4,则A(-2,0),B(4,0),
直线y=x-10坐标轴的交点为C、E,如图,则C(10,0),E(-10,0),
∴△OCE为等腰直角三角形,
∴∠OCE=45°,
作B点关于CE的对称点D,如图,则∠DCE=∠BCE=45°,
∴△BCD为等腰直角三角形,
∴CD=BC=10-4=6,
∴D(10,-6),
连结AD交CE于M,连结MB,如图,
∵BM=MD,
∴MA+MB=MA+MD=AD,
∴此时MA+MB最小,
设直线AD的解析式为y=kx+b,
把A(-2,0),D(10,-6)代入得$\left\{\begin{array}{l}{-2k+b=0}\\{10k+b=-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-1}\end{array}\right.$,
∴直线AM的解析式为y=-$\frac{1}{2}$x-1.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程;△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了待定系数法求一次函数解析式.解决本题的关键是确定B点关于直线y=x-10的对称点D的坐标.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
 如图,一次函数y=$\frac{2}{3}$x-2的图象分别与x轴.y轴交于点A.B,以线段AB为边在第四象限内作等腰Rt△ABC,∠BAC=90°,求过B、C两点直线的解析式.
如图,一次函数y=$\frac{2}{3}$x-2的图象分别与x轴.y轴交于点A.B,以线段AB为边在第四象限内作等腰Rt△ABC,∠BAC=90°,求过B、C两点直线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
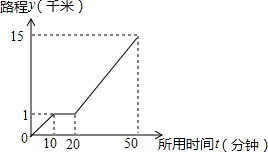 万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )
万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )| A. | 小强家与小明家的路程为1千米 | |
| B. | 小强在小明家楼下的公共汽车站等10分钟 | |
| C. | 该公共汽车的平均速度为30 千米/小时 | |
| D. | 他们乘公共汽车用了30分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${({2\sqrt{3}})^2}=2×3=6$ | B. | $\frac{{\sqrt{8}}}{2}=\sqrt{4}=2$ | C. | $\sqrt{(-9)×(-4)}$=$\sqrt{36}$=6 | D. | $\sqrt{9+16}=\sqrt{9}+\sqrt{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com