
【题目】如图,是一张平行四边形纸片ABCD(AB<BC),要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:对于甲、乙两人的作法,可判断( )

A.甲、乙均正确B.甲、乙均错误C.甲正确,乙错误D.甲错误,乙正确
【答案】A
【解析】
首先证明△AOE≌△COF(ASA),可得AE=CF,再根据一组对边平行且相等的四边形是平行四边形可判定判定四边形AECF是平行四边形,再由AC⊥EF,可根据对角线互相垂直的四边形是菱形判定出AECF是菱形;四边形ABCD是平行四边形,可根据角平分线的定义和平行线的定义,求得AB=AF,所以四边形ABEF是菱形.
甲的作法正确;

∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵EF是AC的垂直平分线,
∴AO=CO,
在△AOE和△COF中,
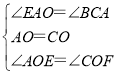 ,
,
∴△AOE≌△COF(ASA),
∴AE=CF,
又∵AE∥CF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形;
乙的作法正确;
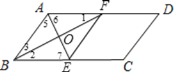
∵AD∥BC,
∴∠1=∠2,∠6=∠7,
∵BF平分∠ABC,AE平分∠BAD,
∴∠2=∠3,∠5=∠6,
∴∠1=∠3,∠5=∠7,
∴AB=AF,AB=BE,
∴AF=BE
∵AF∥BE,且AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴平行四边形ABEF是菱形;
故选:A.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
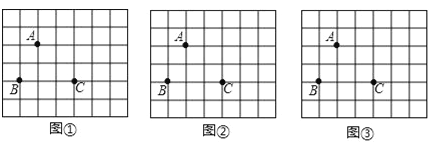
【题目】如图,均为7×6的正方形网格,点A、B、C均在格点(小正方形的顶点)上,在图中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其满足下列条件(三个图形互不相同):
(1)在图①中所画的四边形中,∠D为钝角,且四边形是轴对称图形.
(2)在图②中所画的四边形中,∠D为锐角,且四边形是中心对称图形.
(3)在图③所画的四边形中,∠D为直角,且四边形面积为5平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移得到△A1B1C1的面积.求:
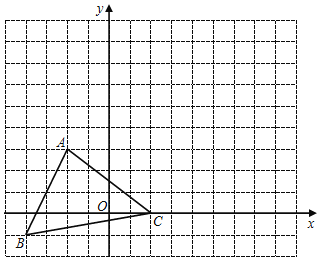
(1)画出△A1B1C1和写出点B1的坐标;
(2)写出平移的过程;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,D是AC的中点,CE⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为( )

A. 40 B. 46 C. 48 D. 50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com