
【题目】已知PA与⊙O相切于点A,B、C是⊙O上的两点
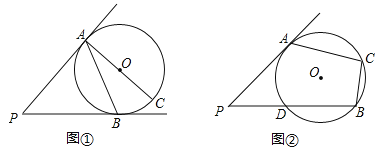
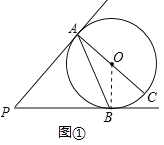
(1)如图①,PB与⊙O相切于点B,AC是⊙O的直径若∠BAC=25°;求∠P的大小
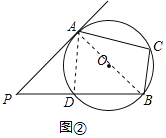
(2)如图②,PB与⊙O相交于点D,且PD=DB,若∠ACB=90°,求∠P的大小
【答案】(1)∠P=50°;(2)∠P=45°.
【解析】
(1)连接OB,根据切线长定理得到PA=PB,∠PAO=∠PBO=90°,根据三角形内角和定理计算即可;
(2)连接AB、AD,根据圆周角定理得到∠ADB=90°,根据切线的性质得到AB⊥PA,根据等腰直角三角形的性质解答.
解:(1)如图①,连接OB.
∵PA、PB与⊙O相切于A、B点,
∴PA=PB,
∴∠PAO=∠PBO=90°
∴∠PAB=∠PBA,
∵∠BAC=25°,
∴∠PBA=∠PAB=90°一∠BAC=65°
∴∠P=180°-∠PAB-∠PBA=50°;
(2)如图②,连接AB、AD,
∵∠ACB=90°,
∴AB是的直径,∠ADB=90·
∵PD=DB,
∴PA=AB.
∵PA与⊙O相切于A点
∴AB⊥PA,
∴∠P=∠ABP=45°.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
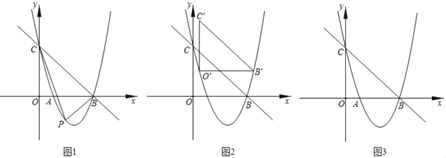
【题目】如图1,抛物线y=ax2﹣![]() x+c交x轴于A,B两点,交y轴于点C.直线y=﹣
x+c交x轴于A,B两点,交y轴于点C.直线y=﹣![]() x+3经过点B,C.
x+3经过点B,C.
(1)求抛物线的解析式;
(2)若点P为直线BC下方的抛物线上一动点(不与点B,C重合),则△PBC的面积能够等于△BOC的面积吗?若能,求出相应的点P的坐标;若不能,请说明理由;
(3)如图2,现把△BOC平移至如图所示的位置,此时三角形水平方向一边的两个端点点O′与点B′都在抛物线上,称点O′和点B′为△BOC在抛物线上的一“卡点对”;如果把△BOC旋转一定角度,使得其余边位于水平方向然后平移,能够得到这个三角形在抛物线上新的“卡点对”.请直接写出△BOC在已知抛物线上所有“卡点对”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c过等腰Rt△OAB的A,B两点,点B在点A的右侧,直角顶点A(0,3).
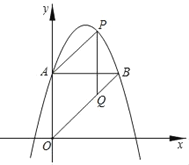
(1)求b,c的值.
(2)P是AB上方抛物线上的一点,作PQ⊥AB交OB于点Q,连接AP,是否存在点P,使四边形APQO是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出利用尺规作图完成下面问题:已知:△ABC是⊙O的内接三角形.求作:△ABC中∠BAC的平分线.
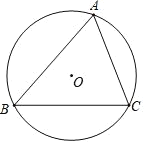
小明的作法如下:
(1)作BC边的垂直平分线DE,交BC于点D,交弧BC于点E;
(2)连接AE,交BC边于点F;则线段AF为所求△ABC中∠BAC的平分线.根据小明设计的尺规作图过程,
①在图中补全图形(尺规作图,保留作图痕迹);
②完成下面的证明.
证明:∵OB=OC,DE是线段BC的垂直平分线
∴圆心O在直线DE上( ).
∵DE⊥BC,
∴![]() ( ).
( ).
∴∠BAE=∠CAE( ),
∴线段AF为所求△ABC中∠BAC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=60°,点O为AB上一点,且3AO=AB,以OA为半径作半圆O,交AC于点D,AB于点E,DE与OC相交于F.
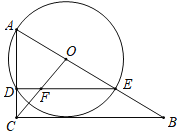
(1)求证:CB与⊙O相切;
(2)若AB=6,求DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
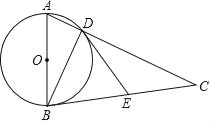
【题目】如图,在锐角△ABC中,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线DE交边BC于点E,连结BD.
(1)求证:∠ABD=∠CDE.
(2)若AC=28,tanA=2,AD:DC=1:3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,点 D 为边 BC 的点,点 E、F 分别是边 AB、AC 上两点,且 EF∥BC,若 AE:EB=m,BD:DC=n,则( )
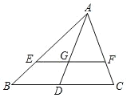
A.若 m>1,n>1,则 2S△AEF>S△ABDB.若 m>1,n<1,则 2S△AEF<S△ABD
C.若 m<1,n<1,则 2S△AEF<S△ABDD.若 m<1,n>1,则 2S△AEF<S△ABD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com